С появлением карвинговых лыж радиус бокового выреза стал стремительно уменьшаться. Появилось всем ныне известное слово Sidecut и радиус бокового выреза стал одним из основных параметров лыжи. Радиус стал указываться в каталогах, инфоблоке на лыжах и резко стал интересен всем. FIS стала регламентировать его величину, а любители — спорить о его значении. )))
Связь сайдката и радиуса дуги резаного поворота тоже была вычислена. Следует заметить, что эта формула включает ряд ограничений и служит скорее для оценки получаемой дуги. Появились некоторые «калькуляторы», позволяющие самому рассчитать величину радиуса бокового выреза. И вот тут стали возникать недоразумения. Полученный радиус, как правило, не совпадал с указанным на лыже.
Попробуем разобраться, в чем же дело.
На первый взгляд расчет радиуса бокового выреза — достаточно простая операция. Имея ширину носка, пятки, талии и длину лыжи, можно посчитать радиус прогиба боковой поверхности по приближенной формуле
R=L L: 8h
где L –длина хорды (лыжи), а h - величина максимального прогиба (стрелка прогиба)
Однако не все так просто.
Дело в том, что форма бокового выреза, как правило, не является дугой окружности. Для условий чистого резаного ведения это должна быть кривая, дающая в проекции на плоскость склона при прогибе лыжи кривую, максимально приближенную к дуге окружности. Только в этом случае все точки канта будут проходить один путь и резание станет максимально чистым. Сразу скажу, что это условие на практике, как правило, не может точно соблюдаться в силу различных причин, о которых здесь пока говорить не будем.
Максимально точно всем этим требованиям отвечают некоторые кривые второго порядка.
Например, парабола.
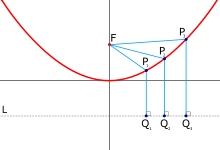
Надо сказать, что лыжи с параболическим вырезом использовала фирма Elan еще в начале века. Она выпускала одни из первых радикальных карверов Elan Parabolic.
Так причем же здесь радиус окружности, указываемый на лыжах?
Дело в том, что парабола на небольшом участке своей длины может быть аппроксимирована окружностью с соответствующим радиусом. Например, в точке апекса этот радиус равен фокальному параметру (p) и может быть легко выделен из уравнения параболы (y2=2px, p>0 ). Подобная аппроксимация возможна и для других кривых второго порядка. Однако, когда мы имеем достаточно протяженную дугу, то радиус по ней становится переменным и, естественно, не совпадает с вычисленным «калькулятором».
Интересен боковой вырез в форме эллипса.
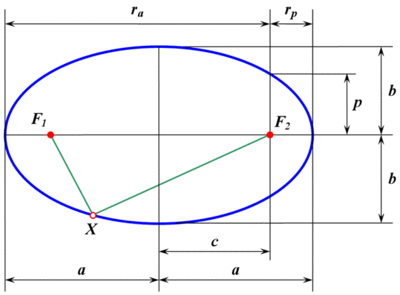
Поскольку эллипс — это общий случай окружности, то любая точка на этой кривой имеет свой радиус. Становится понятным, что, выбирая соответствующие участки эллипса, можно получить как уменьшение радиуса к концам лыжи, так и его увеличение.
Возможно так же использование и других кривых. Фирмы, как правило, неохотно рассказывают о своих геометрических изысканиях. Особенно любят секретить точную геометрию спортивных лыж. При этом надо понимать, что простыми промерами эту геометрию определить невозможно.
Несмотря на некоторую неточность, указываемый радиус дает примерное представление о кривизне боковины лыжи.
Надо сказать, что боковой вырез в форме дуги окружности тоже используется в простых моделях лыж.
Последнее время появилось много моделей лыж, где используются два или более радиуса. Надо сказать, что тут фирмы уже стараются указывать все используемые радиуса. Это и модели от Fischer серии Progressor, у которых радиус носка значительно меньше радиуса середины и хвоста лыжи. И Head Rev (у которого радиус носка на 20% меньше) и некоторые другие модели.
Некоторые фирмы используют еще большее количество радиусов. Например, Scott в технологии 3DSidecut использует различные радиуса носка и пятки и участок прямой между ними. А Line в технологии 5CUT, вообще использует 5 (!) различных радиусов.
Естественно, получить сходство посчитанного радиуса и реального в таких условиях практически невозможно!
17 часов же не докатал по здоровью разбитой бошки) И рыть себе трассы тоже чем то надо , не спичками же ?
