В статье рассмотрена биомеханическая модель движения тела лыжника, с помощью которого лыжник может за счет мышечного усилия эффективно управлять скоростью и степенью закантовки лыж, а также их врезанием в склон.
ВВЕДЕНИЕ
Вопрос достижения больших углов закантовки лыж в энергетическом смысле аналогичен вопросу о бросании камня вверх на максимальную высоту. Движению камня «мешает» сила тяжести и результат бросания зависит от начальной скорости камня. Максимальный угол закантовки лыж зависит от скорости, с которой лыжник «бросает» свое тело в поворот поперек траектории лыж. Наклону лыжника в поворот сильно «мешает» центробежная сила, но немного «помогает» сила тяжести.
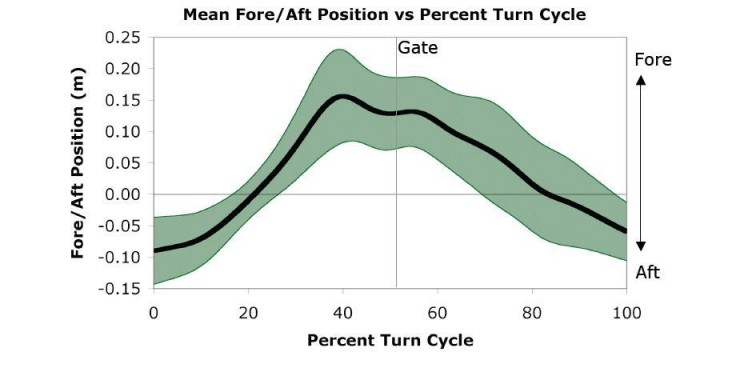
Скорость, с которой лыжник пересекает траекторию лыж в момент «плоских лыж», зависит от величины центробежной силы в предыдущем повороте. Известно, что скорость в активной дуге резаного поворота спортсмена заметно уменьшается во второй половине дуги (Reid 2010). Поэтому центробежная сила также уменьшается и лыжник должен каким-то образом увеличивать кинетическую энергию своего движения поперек траектории лыж в конце активной дуги. Иначе он не сможет достичь в новом повороте такого же угла закантовки, как и в «старом» повороте по чисто энергетическим соображениям.
Все сказанное справедливо с одной оговоркой – лыжи должны надежно резать склон. Когда последнее условие не выполняется, то вопрос о достижении больших углов закантовки лыж для такого лыжника не актуален. Влияние силы тяжести «перевесит» влияние центробежной силы и лыжник упадет на бок. Если же лыжи надежно режут склон, то даже при не очень большой скорости движения лыжнику не даст упасть на склон центробежная сила. Она будет мешать достижению больших углов закантовки и выталкивать лыжника в новый поворот. Подробнее об этом рассказано в статье "Эффект «упругого склона» («шеста») используется восходящей звездой Кубка мира Alice Robinson в ее технике. И это подтверждает ее тренер"
Интуитивно понятно, что для достижения больших углов закантовки лыж, лыжнику нужно активнее «подавать» или даже "бросать" свой центр масс в новый поворот поперек движения лыж. Но вопрос «как именно подавать?» не разрешен до сих пор.
Еще в 70-х Bear (1976) предложил рассматривать концепцию «расхождения» (divergence) траекторий лыж и лыжника как «ожидание» (anticipation). Он выдвинул идею о том, что расхождение траекторий лыж и лыжника требует от лыжника моментального «падения» в поворот в ожидании (anticipation) возникновения последующей реакции склона, по аналогии с механизмом прямохождения человека. Le Master (2009) предположил, что такая способность «падать» в каждый новый поворот именно в той мере в которой это необходимо – не слишком сильно и не слишком слабо – является навыком, отличающим продвинутых лыжников.
Major & Larson (1979/1979) отмечали, что широкая постановка ног способствует достижению нужного начального угла наклона ЦМ в поворот, так как переступание на новую внешнюю лыжу в ходе транзита между поворотами в этом случае обеспечивает заметный начальный наклон (inclining) ЦМ в поворот (Bear 1976, Le Master 1999).
Однако, прямые измерения давления на лыжи, которое оказывают лыжники уровня КМ в повороте гигантского слалома показали, что в самом начале и в самом конце активной дуги (первые и последние 20% активной дуги соответственно) элитные лыжники загружают обе лыжи с одинаковой интенсивностью - в соотношении практически 50х50 (Meyer, Prenleloup, Schorderet (2012)). Это противоречит гипотезе «простого «сваливания» путем переступания на новую внешнюю лыжу, выдвинутой в профильной литературе (Major & Larson (1979/1979), Bear 1976, Le Master 1999).
Тем не менее, в качестве базовой биомеханической модели для движения «подачи» в поворот исследователи рассматривали «простое «сваливание» тела лыжника вбок (Morawski 1973, Bear 1976, Major & Larson 1979/1979, Le Master 1999) при потере лыжником равновесия вследствие расслабления мышц - разгибателей одной ноги. Однако, это движение было «забраковано», в частности, Ж. Жубером (Joubert (1978/1980), как слишком медленное. Для узкого ведения это время «простого «сваливания» составляло от 0,5 до 1 секунды (Morawski 1973, Lindt & Sanders 2004), что давало право утверждать, что при выполнении обычных поворотов лыжник должен использовать дополнительные механизмы, ускоряющие наклон.
Joubert (1978/1980) отмечал, что если «сваливание» необходимо ускорить в области таза, то, расслабив указанные мышцы, нужно еще подтянуть ноги к туловищу (сгибание углом в боковом плане тела). В этом случае вместе с наклоном происходит угловое движение. Но теоретический анализ биомеханики подобного движения не производился.
Joubert (1978/1980) отмечал также, что «сваливание» можно ускорить путем увеличения начальной скорости сваливания. Для чего предлагалось «усиливать» динамику предыдущего поворота - делать небольшой подскок, направленный вбок-вверх по склону, для перекантовки; делать предповорот; разворачивать и устремлять лыжи вверх по склону, в то время как лыжник продолжает двигаться в прежнем направлении (скользящий толчковый поворот и поворот авальманом).
Никто из исследователей не обратил внимания на то, что совершая активное разгибательное движение при наличии ангуляции, как бедренной, так и коленной, лыжник силой своих мышц может напрямую оказывать заметное влияние на динамику «подачи» своего ЦМ в поворот. Как следствие, лыжник может оказывать заметное влияние на динамику закантовки лыж и на величину максимального угла закантовки. При этом лыжник использует почти те же группы мышц, которые используются, например, при прыжке с места - мышцы ног и кора, но с одной оговоркой. Лыжник избегает махов руками, а движению его стоп препятствуют горнолыжные ботинки.
Активное разгибательное/сгибательное движение оказывает заметное влияние на динамику «подачи» своего ЦМ в поворот даже тогда, когда лыжник использует очень узкую стойку или вообще едет на одной лыже (монолыже). На первый взгляд это противоречит тому, что в безопорном состоянии никакие движения лыжника не оказывают влияния на движение его центра масс, что является прямым следствием закона сохранения импульса. Однако если лыжник имеет даже точечную опору, то движение ЦМ лыжника будет зависеть от интенсивности движений тела лыжника, например, интенсивности движения ангуляции, что непосредственно следует из закона сохранения момента импульса и не противоречит закону сохранения импульса.
Для нефизиков, предпочитающих объяснения «по аналогии», можно говорить об аналогии с динамикой гребли веслом или динамики плавания. Для наглядности можно назвать эту аналогию, например, «эффектом весла»
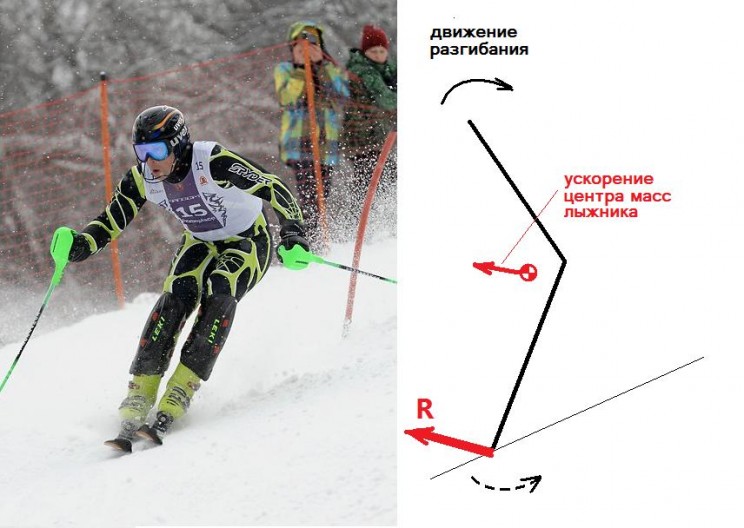
«Эффект весла» возникает, например, когда лыжник интенсивно разгибается во второй половине резаного поворота. Лыжник как бы использует нижнюю часть своего тела в качестве «весла», к которому он прикладывает мышечные усилия, и совершает «гребок» для перемещения своего центра масс в нужном направлении. КПД такого движения разгибания, как бедренной так и коленной ангуляции, в направлении «поперек движения лыж» составляет примерно 60%. Этот КПД максимален когда лыжник согнут не очень сильно и равен нулю, если тело лыжника «согнуто под прямым углом». Примерно 40% мощности, которую развивает лыжник при разгибании своего тела, пойдет на создание «ненужного» вращения верхней и нижней частей его тела вокруг центра масс лыжника, но остальные 60% усилий пойдут на благое дело дополнительной «подачи» ЦМ в поворот.
Из закона сохранения момента импульса следует, что в безопорном состоянии движения нижней и верхней частей лыжника происходили бы с примерно одинаковыми угловыми скоростями и ускорениями. Наличие же склона мешает движению нижней части тела лыжника и не позволяет ей перемещаться в желаемом направлении. Возникает дополнительная сила реакции склона R, которая и «толкает» центр масс лыжника в направлении поперек лыж.
Дополнительное ускорение ЦМ лыжника в направлении «поперек движения лыж», которое создается за счет мышечных усилий лыжника, может быть сравнимо с ускорением свободного падения – 9.8м/с2, а усилие, которое лыжник своими мышцами передает на лыжи в обсуждаемом здесь направлении равно примерно весу лыжника в покое. Это усилие обеспечивает надежное врезание лыж. Значение этого факта для стабильности врезания я подробно разбирал в статье "Зачем лыжнику ангуляция? О максимально возможном угле закантовки лыжи. И о том, что ангуляции много не бывает!"
Действительно, величина суммарного изометрического момента, который развивает средний человек при разгибании в коленях (408 Н*м), бедрах (300 Н*м) и корпусе (258 Н*м) составляет около 960 Н*м (Knudson 2007). Расстояние от лыж до центра масс лыжника для спортивного стиля езды составляет примерно 70 см (Reid 2010). Поэтому ускорение центра масс лыжника, которое дает «эффект весла» с учетом его КПД в 60% составляет 11.7 м/с2 (масса лыжника для оценки - 70 кг). Учет того, что разгибание при ангуляции происходит не «прямо» а «под некоторым углом» дает возможный поправочный коэффициент порядка 0.7 и окончательную оценку для максимального дополнительного мышечного ускорения ЦМ лыжника – 8.2м/с2.
Очевидно, что «эффект весла» возникает только тогда, когда разгибание происходит с некоторым угловым ускорением. Этот эффект исчезает как только лыжник останавливает разгибание или совершает его без ускорения. Эффект продолжается ограниченное время, которое определяется биомеханическими ограничениями – амплитудой сгибания/разгибания, которая составляет 70-80 градусов. Но это время сравнимо с временем поворота, поэтому совместив интенсивное разгибание с окончанием поворота и моментом полной разгрузки, лыжник может добиться того, чтобы дополнительная скорость ЦМ лыжника в направлении «через лыжи» уже после прекращения движения может достигать величины порядка метра в секунду.
Действительно, если лыжник в конце активной дуги начнет разгибаться, развивая максимальный момент, то через 0.1с его ЦМ приобретет дополнительную скорость 0.82 м/с в направлении «поперек лыж» и дополнительно переместится на 4 см в том же направлении. Дополнительное угловое смещение (расклон) ЦМ лыжника относительно лыж составит при этом около 3 градусов.
Необходимо заметить, что эффект от ускорение разгибания полностью аналогичен эффекту от замедления сгибания.
Таким образом, управление скоростью перекантовки с помощью «эффекта весла» в разы эффективнее метода «простого сваливания». Кроме того, при «эффекте весла» лыжник должен с одинаковой интенсивностью использовать обе ноги, так как, если лыжник будет загружать только одну ногу, то «эффект весла» уменьшится почти в два раза. Это полностью согласуется с тем, что в повороте гигантского слалома в самом начале и в самом конце активной дуги (первые и последние 10-20% активной дуги соответственно) элитные лыжники (уровня КМ) загружают обе лыжи с одинаковой интенсивностью - в соотношении практически 50х50 (Meyer, Prenleloup, Schorderet (2012)).
«Эффект весла», в частности, дает ответ на вопрос каким образом лыжник может быстро выйти из равновесной резаной дуги, например, в фанкарвинге.
Понимание механизма «эффекта весла» позволяет по новому взглянуть на общее значение ангуляции в горнолыжной технике как на ключевой технический элемент, позволяющим лыжнику управлять как скоростью и степенью закантовки лыж, так и их врезанием.
В настоящее же время ангуляция рассматривается как чисто вспомогательный технический прием. Считается, что с помощью техники ангуляции лыжник может в некоторых пределах регулировать угол закантовки лыж независимо от наклона своего центра масс (Lindt & Sanders 2004, Le Master 1999). Исследователи полагают, что наклон или инклинация (inclining) ЦМ в поворот происходит в основном за счет расхождение траекторий лыж и лыжника и является основным фактором, определяющим закантовку лыж (Whitherell 1972) и, поэтому, играет решающую роль в определении радиуса поворота. Тот факт, что интенсивное ангуляционное движения может существенно влиять на степень расхождения траекторий лыж и лыжника, ускользнул от внимания исследователей.
Представляется, что общая существенная недооценка методистами, тренерами и лыжниками роли ангуляции как технического приема ведет к существенному замедлению скорости повышения технического уровня лыжников или к стагнации этого уровня.
ОПИСАНИЕ МОДЕЛИ
(Этот раздел написан конспективно и предназначен для интересующихся физическим обоснованием выводов данной статьи, его можно пропустить без ущерба для общего понимания и переходить к разделу ОБСУЖДЕНИЕ)
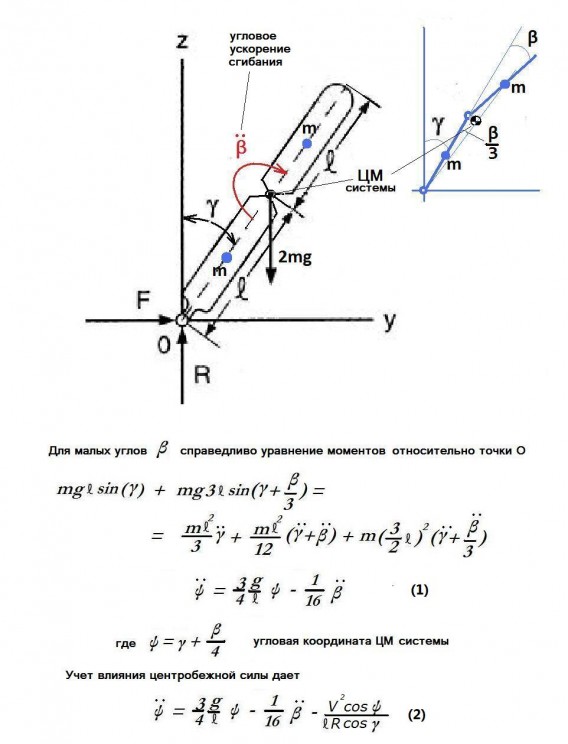
Рассмотрим двухзвенную моделью тела лыжника. Представим лыжника как систему двух одинаковых абсолютно жестких стержней массой m и длиной l каждый, соединенных шарниром. Будем считать, что стержни взаимодействуют друг с другом. Это взаимодействие выражается в том, что на каждый стержень со стороны другого стержня действует некоторый «внутренний» момент Р. Момент Р создают мышечные усилия лыжника. Под действием этого момента стержни могут двигаться друг относительно друга с некоторым угловым ускорением, образовывая угол. Угловое ускорение определяется моментом Р. Трение в системе отсутствует. Движение стержней происходит в нормальной к склону плоскости, перпендикулярной направлению движения лыж. Нижний стержень взаимодействует с поверхностью по типу шарнира и в боковом направлении не проскальзывает.
Рассматриваемая системя является усложненным вариантом модели «перевернутый маятник» (Morawski 1976). Рассмотрим, как и Morawski 1976 движение системы под действием только силы тяжести. Но учтем мышечные усилия лыжника, который развивает некоторое угловое ускорение сгибания/разгибания.
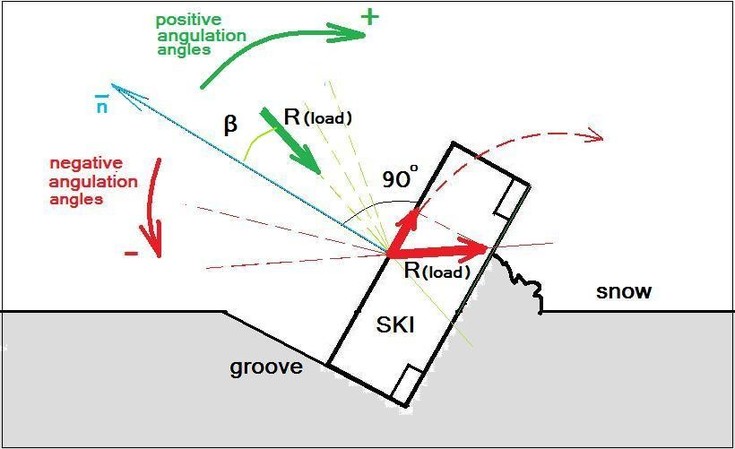
В полученных уравнениях 1 и 2 две точки над символом означает вторую производную по времени, а направление "по часовой стрелке" является положительным направлением. То есть, если верхнему стержню сообщается угловое ускорение в указанном красной стрелкой направлении, то "эффект весла" работает против силы тяжести.
Так, если начальный угол наклона системы γ равен 30 градусам (около 0.5 радиана), то ЦМ системы не будет "падать" если верхнему стержню сообщается угловое ускорение в примерно 80 рад/с2 в указанном красной стрелкой направлении. Однако, это равновесие продлится недолго, примерно 0.2 с. Это время определяется максимальной угловой амплитудой движения верхнего стержня относительно нижнего, которая имеет биомеханический смысл. Очевидно, что эта амплитуда составляет не более 180 градусов.
Полученное выше уравнение (1) для углового ускорения ЦМ системы очень похоже на уравнение, полученное Morawski 1973 (Приложение 1). Отличие совсем «небольшое» - наличие второго слагаемого в правой части уравнения. Как было показано выше, величина этого слагаемого выражает активные действия лыжника. Видно, что, в отличие от модели Morawski 1973 (Приложение 1), в зависимости от величины и направления углового ускорения сгибания/разгибания величина ускорения ЦМ системы может существенно изменяться, как увеличиваться, так и уменьшаться- "эффект весла". Но,как было показано, чем существенней действие "эффекта весла", тем меньше время его "существования".
Из уравнений 1 и 2 видно, что "эффект весла" исчезает, если угловое ускорение движения сгибания/разгибания равно нулю, то есть это движение происходит с постоянной скоростью или оно вообще не происходит. Максимальная величина углового ускорения сгибания/разгибания лыжника зависит от мышечных усилий лыжника (максимального изометрического момента, развиваемого лыжником) и КПД «эффекта весла».
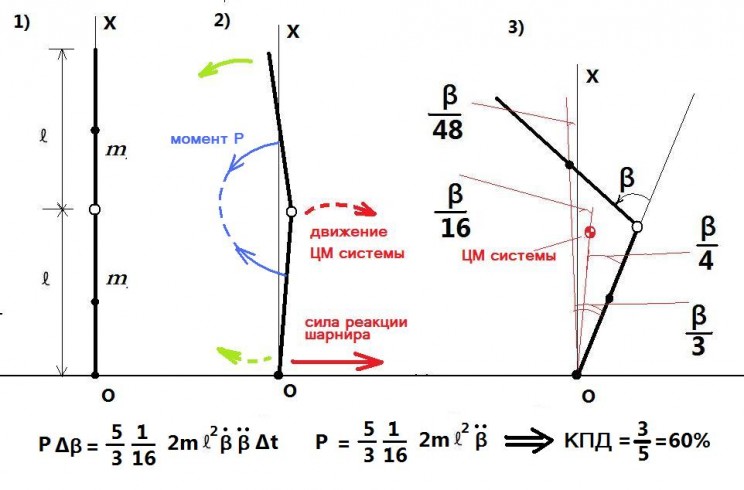
Для оценки КПД «эффекта весла» следует рассмотреть движение системы только под действием усилий лыжника, создающего момент Р, в отсутствие силы тяжести и сил инерции. Общий момент импульса системы относительно точки О (шарнира) является постоянной величиной. С учетом уравнения для связей, получим для малых углов β (меньше 30 градусов) следующий результат.
Указанные соотношения выполняются для угловых ускорений стержней, их центров масс и углового ускорения ЦМ системы в любой момент времени и не зависит от начальных углов и скоростей в системе.
Таким образом, угловое ускорение ЦМ системы при указанном ангуляционном движении примерно в 16 раз меньше, чем угловое ускорение верхней части тела лыжника относительно его нижней части. Аналогично, последне ускорения определяет и ускорения ЦМ каждого стержня , а также угловые ускорения движения стержней относитеьно их ЦМ.
Работа момента Р идет на приращение кинетической энергии движения ЦМ каждого стержня и кинетической энергии вращения стержней относительно своих ЦМ. Из сказанного, а также из указанных на рисунке соотношений угловых ускорений и уравнения движения ЦМ системы получим КПД «эффекта весла» - а именно, что 60% мощности затрачиваемой лыжником на угловое ускорение верхней части тела лыжника относительно его нижней части идет на создание дополнительного ускорения его ЦМ.
Используя представленные выше выкладки, аналогичные результаты можно получить и для двухзвенной биомеханической модели коленной ангуляции. Уравнение движения ЦМ для этого случая практически совпадает с полученным выше уравнением для бедренной ангуляции. КПД для модели коленной ангуляции составляет 64%.
Уравнения динамики линейны, поэтому уравнение движения ЦМ для трехзвенной модели лыжника, совмещающего бедренную и коленную ангуляцию получается простым добавлением в правую часть полученного выше уравнения слагаемого, которое выражает влияние углового ускорения коленной ангуляции. Вид этого слагаемого практически эквивалентен слагаемому для бедренной ангуляции. КПД совместного ангуляционного движения в бедрах и коленях составляет примерно 60% для малых углов «сгибания».
ОБСУЖДЕНИЕ
«Эффект весла» заметно проявляется только если лыжник очень резко совершает ангуляционное движение – сгибается или разгибается. Причем ускорение разгибания создает точно такой же эффект как и торможение сгибания, так как направление углового ускорения для этих двух случаев является одинаковым. Поэтому торможение сгибания вплоть до его остановки в апексе поворота и последующее ускорение разгибания создают достаточно длительный период надежного врезания лыж.
Здесь можно упомянуть упражнение "хоккейная остановка". В этом упражнении лыжник путем резкого торможения ангуляционного сгибательного движения, добивается сильного врезания кантов лыж в склон, которое вызывает резкую остановку.
В случае спортивных поворотов «очень резко» - означает что полная амплитуда движения совершается за 0.2-0.3 с. Примерно это мы наблюдаем в поворотах ведущих лыжников КМ, которые полностью «складываются» в первой половине дуги примерно за 0.2-0.3 с. Лыжники начинают "складываться" когда их лыжи уже закантованы на заметный угол, а тело относительно выпрямлено и наклонено в новый поворот. Это сокращает время складывания и многократно усиливает возможности лыжника управлением закантовкой и врезанием лыж - "эффект весла".
Если лыжник придерживается правила «вертикальный корпус» в течение всей дуги любительского поворота, полудуга которого длится больше 0.5-0.6 с который , то есть, если лыжник начинает «складываться» сразу после момента «плоские лыжи», то «эффект весла» в этом случае ослабевает в разы. Это приводит к проблемам с врезанием лыж в течение всей дуги поворота. Статическая ангуляция начинает положительно влиять на врезание лыж только тогда, когда тело лыжника имеет заметное угловое положение. Для статического случая правила "вертикальный корпус" статическая ангуляция начинает положительно влиять на врезание лыж когда уголзакантовки лыж превышает примерно 30-35 градусов. Поэтому при малых углах закантовки в этом случае лыжник будет испытывать проблемы с врезанием лыж.
Таким образом ангуляция теряет свою эффективность, если лыжник "размазывает" движение ангуляции во времени больше чем на 0.4-0.5 с. В этом случае "эффект весла" практически исчезает. Чем короче промежуток времени за который лыжник "складывается" или распрямляется, тем значительней "эффект весла" и тем больше эффект от ангуляции, как технического приема.
Поэтому продвинутые лыжники и эксперты при катании придерживаются той же тактики, что и ведущие лыжники КМ. Эксперт увеличивает период разгруженного состояния лыж и это позволяет ему более надежно и сильно врезать лыжи в склон в более короткий период загрузки лыж, пользуясь также и "эффектом весла". Механизм этого явления объяснен в статье "Что должен делать лыжник, чтобы его лыжи надежно резали склон."
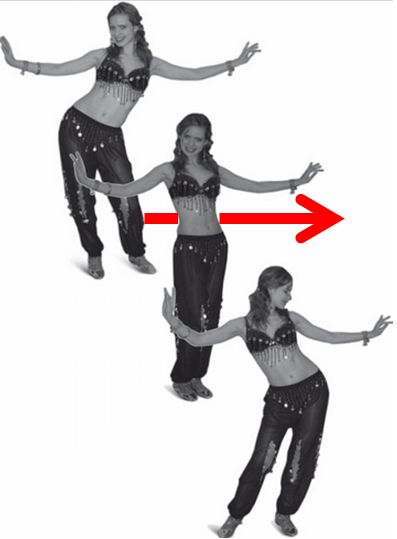
При выполнении короткого резаного поворота эксперт проходит момент "плоских лыж" в безопорном состоянии (положение 1 - лыжи не касаются склона). Лыжи ставятся на склон уже заметно закантованными, при этом тело лыжника относительно выпрямлено и при загрузке лыж лыжник начинает сгибательное ангуляционное движение (положение 2). Путем интенсивного торможения ангуляционного сгибания (положение 3) лыжник добивается надежного врезания в апексе поворота, которое создает надежную опору и позволяет ему интенсивно разогнуться во второй половине поворота и управляемо "бросить" свое тело в следующий поворот, то есть перейти в следующий поворот с полным контролем поперечной скорости (поперечной к направлению движения лыж).
Какие группы мышц нужно тренировать для улучшения динамики ангуляции и какие упражнения для этого нужно делать? Очевидно, что речь идет о мышцах ног и кора в широком смысле и об упражнениях ОФП связанных с тренировкой общей гибкости и тренировкой указанных групп мышц. Также очевидно, что хорошей тренировкой являются всевозможные поддержания равновесий - на ленте, мяче и прочее. Но в случае аналогии с лыжником меется специфика - движение стоп блокируется ботинками, движение рук не приветствуется. Поэтому в качестве СФП, возможно, подойдет упражнение типа стояния на мяче в горнолыжных ботинках или прыжков вбок на дальность с двух ног при узкой постановке этих ног, обутых в горнолыжные ботинки и без какой-либо помощи рук.
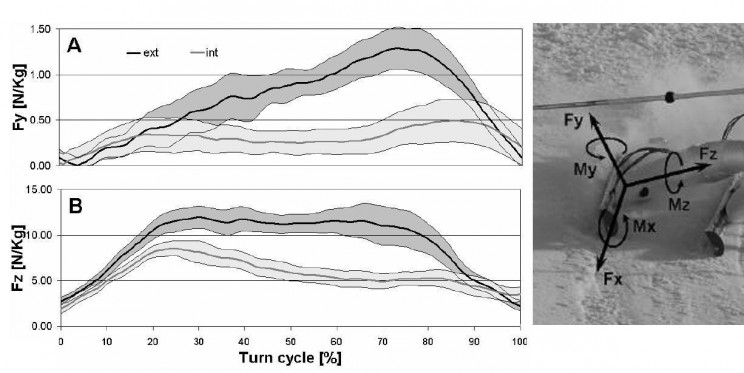
Использование лыжниками уровня КМ «эффекта весла» имеет экспериментальное подтверждение. Для времени "складывания" тела лыжника за 0.3 с на угол 70 градусов (примерно 1.2 радиан) среднее угловое ускорение складывания будет составлять примерно 27 рад/с2. Дополнительное угловое ускорение движения ЦМ будет составлять примерно в 16 раз меньшую величину - 1.7 рад/с2. Линейное ускорение ЦМ с учетом плеча в 0.7м будет равно 1.2м/с2. Это будет выражаться в наличии дополнительной силы реакции склона равной 12% от веска лыжника в покое и направленной поперек лыж и параллельно их скользящей поверхности. Полученный результат неплохосогласуется с экспериментальными данными Meyer, Prenleloup, Schorderet (2012)
Meyer, Prenleloup, Schorderet (2012) зафиксировали заметное усилие, которым лыжники уровня КМ загружают лыжи в направлении поперек движения лыж и параллельном скользящей поверхности. Причем, это усилие было максимальным в конце активной дуги ГС поворота и составляло около 15% веса лыжника в покое, что объясняется активным разгибанием лыжников в конце дуги.
Также, как говорилось выше, прямые измерения давления на лыжи, которое оказывают лыжники уровня КМ в повороте гигантского слалома показали, что в самом начале и в самом конце активной дуги (первые и последние 20% активной дуги соответственно) элитные лыжники загружают обе лыжи с одинаковой интенсивностью - в соотношении практически 50х50 (Meyer, Prenleloup, Schorderet (2012)).
Выше говорилось, что при «эффекте весла» лыжник должен с одинаковой интенсивностью использовать обе ноги, так как, если лыжник будет загружать только одну ногу, то «эффект весла» уменьшится почти в два раза. Это полностью согласуется с результатом Meyer, Prenleloup, Schorderet (2012).
ПРИЛОЖЕНИЕ 1.
СПИСОК ЛИТЕРАТУРЫ
Knudsen D. "Fundamentals of Biomechanics" 2007.
Остальные ссылки даны в соответствии со списком литературы в работе Reid 2010, а также в статье "Внутренняя лыжа или внешняя? Элитный ГС поворот в цифрах и инструкторские мифы"















Интересная статья. Спасибо