При катании на горных лыжах вопрос контроля скорости - это вопрос № 1 для любого лыжника. 100% лыжников задают себе этот вопрос и пытаются, так или иначе, найти на него ответ, но оказавшись, на крутом склоне 95% лыжников понимают, что ответа на этот вопрос они все еще не знают.
В статье будет показано, что ответ на этот вопрос звучит парадоксально - чем чище лыжник выполняет резаный поворот, тем больше у него возможностей для контроля скорости своего движения, так как с точки зрения физики в самой "естественной" динамике резаного поворота заключены мощные средства контроля скорости движения лыжника, связанные с механизмом формирования идеального карвингового следа и с возможностью влияния на этот механизм активных действий лыжника.
В статье будет показано, что ответ на этот вопрос звучит парадоксально - чем чище лыжник выполняет резаный поворот, тем больше у него возможностей для контроля скорости своего движения, так как с точки зрения физики в самой "естественной" динамике резаного поворота заключены мощные средства контроля скорости движения лыжника, связанные с механизмом формирования идеального карвингового следа и с возможностью влияния на этот механизм активных действий лыжника.
Прямые измерения, произведенные профильными учеными (Рейд (2010)), показывают, что спортсмены, находясь в активной дуге резаного поворота тормозят с таким же СРЕДНИМ ускорением с каким будет тормозить автомобиль на мокрой дороге с аналогичным уклоном. А максимальное ускорение торможения спортсмена в дуге резаного поворота превышает скорость торможения автомобиля на СУХОЙ асфальтированной дороге с аналогичным уклоном. Разве это возможно?
Конечно это возможно. Если вспомнить решение школьной задачи о движении тела по наклонной плоскости, то, учитывая, что коэффициент трения шин о мокрый асфальт равен 0,35-0,45, то можно оценить, что автомобиль будет скользить по мокрому асфальту с 300 уклоном, так как сила трения не сможет удерживать его от соскальзывания и скорость его скольжения будет увеличиваться. При этом высококлассный лыжник свободно проходит резаным поворотом спортивную трассу на ледяном склоне с таким же 300 уклоном и сохраняет нужную ему среднюю скорость своего движения примерно постоянной.
Очевидно, что сила, которая тормозит лыжника в активной дуге, имеет ту же природу, что и сила, действующая на резец при обработке металла резанием. Известно, что чем большее давление резец оказывает на металл, тем больше металла им срезается, тем глубже след от резца и тем больше сила сопротивления резанию. Величина этой силы обусловлена как самой срезкой части металла резцом, так и деформацией оставшегося металла при формировании следа инструмента.
В случае резаного поворота в качестве резца выступает острый кант лыжи, а в качестве металл - склон по которому едет лыжник. При формировании карвингового следа происходит существенная деформация и смещение слоев снега, срезка части снега и его удаление из карвингового следа. Это все можно непосредственно наблюдать на многочисленных слоу мошн видео в интернете. Вот один из вариантов такого видео активой дуги резаного поворота в исполнении одного из лидеров КМ.
Вместе с тем существует устойчивое мнение, что контролировать скорость в чисто резаном повороте вообще невозможно, если не прибегать к помощи проверенных классикой приемов торможения – «сбросу пяток» и тому подобных, не очень одобряемых лыжной общественностью, технических действий.
Часто встречается рекомендация "заезжать вверх по склону" (или "закрывать дугу") в конце поворота, тогда, якобы, скорость лыжника "замедлится сама-собой". Но закон сохранения механической энергии утверждает, что без наличия трения, или иного механизма диссипации энергии, лыжник на склоне будет разгоняться независимо от траектории своего движения, если конечная точка пути лыжника будет расположена ниже начальной точки.
Понятно, что продвинутые лыжники, совершая резаный поворот, каким-то образом контролируют скорость своего движения и не прибегают к «сбросу пяток» даже на ледяном склоне. Но если спросить такого лыжника – что он делает для контроля скорости? – то вразумительного ответа получить не удастся.
Ускорения, с которым замедляется ЦМ спортсмена при движении вдоль активной траектории резаного поворота, не раз измерялись (Рейд (2010) и др.). В апексе резаного поворота, когда фиксируется стадия "чистого каринга", эти ускорения, хотя они и краткосрочные, но достигают 4-4.5 м/с2. как для случая гигантского слалома (Рис.1(а)), так и для слалома (Рейд 2010) (Рис. 1(б)) .
Если учесть влияние "скатывающей силы", например, на 150 склоне, как в экспериментах Рейда, то ускорения с которым замедляется спортсмен в активной дуге резаного поворота достигают 6-7м/с2.
Это просто огромные ускорения. С таким же по величине ускорением тормозит автомобиль на сухом асфальте. Но коэффициент трения шин об асфальт составляет 0.5-0.7, а коэффициент трения лыж о снег равен примерно 0.02.
Как такое возможно? На этот вопрос я не нашел ответа в профильной литературе.
Среднее же «ускорение замедления» ЦМ спортсмена в активной дуге слаломного поворота, которое действует на спортсмена около половины всего времени спуска, оставляет 2-2.5м/с2 . Примерно с таким же ускорением тормозит автомобиль на мокрой дороге, идущей под уклон в 150.
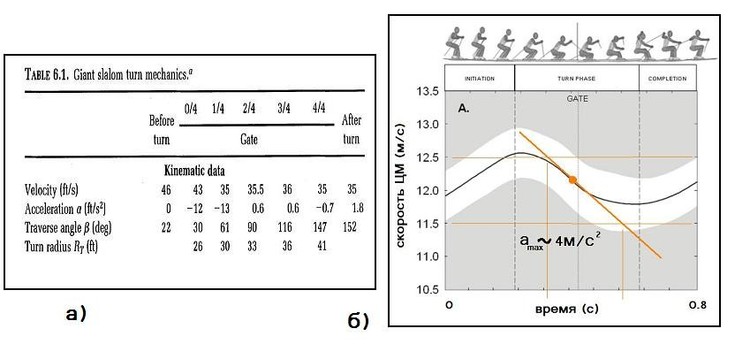
Рис.1 а) – данные из книги «The physics of skiing: Skiing at the triple point» D. Lind, S. Sanders (2004). б) – данные из диссертационной работы (Рейд 2010).
При этом даже с учетом повышенной силы реакции склона, которая действует на спортсмена в апексе резаного поворота и которая превышает вес спортсмена в покое в 3-3.5 раза, вклад в ускорение ЦМ спортсмена, который дает сила трения лыж о снег, не превышает 0.6-0.7 м/с2. Тогда как среднее ускорение ЦМ, которое обеспечивает так называемая «скатывающая сила» составляет для 15-200 склона 2-3 м/с2.
Получается, что эффективный коэффициент трения, которого «добиваются» спортсмены в апексе поворота в 10 и более раз превышает, коэффициент трения лыж о снег, который равен примерно 0.02.
Необходимо отметить, что лыжник своими действиями в повороте может частично уменьшить свою кинетическую энергию (антипампинг). Интегральный вклад этих возможных действий лыжника в замедление его движения является незначительным и может быть сравним с действием силы трения лыж о снег. Но при другом рисунке этих действий лыжник может даже несколько увеличивать скорость своего движения в каждой дуге (пампинг). Указанные действия лыжника я в данной статье рассматривать не буду.
Таким образом, эффективный коэффициент трения лыж спортсменов о лед в апексе резаного поворота сравним с коэффициентом трения шин по асфальту.
Между тем понимание физического механизма, который позволяет лыжнику так сильно тормозить, совершая чисто резаный поворот, необходимо. Это понимание позволит дать рекомендации лыжникам о том, на какие технические действия необходимо обратить внимание, чтобы контролировать скорость в резаном повороте, не прибегая к «сбросу пяток».
Материал, изложенный далее требует от читателя определенных усилий для его понимания и усвоения, а также определенных знаний в области математики и физики.
Те читатели, которых интересуют итоговые выводы и те кто не хочет тратить свое время на чтение этого трудного материала, могут сразу переходить к выводам, которые помещены в конце статьи.
Как я ужеговорил, основное торможение лыж в чисто резаном повороте - это не торможение в обычном понимании, когда, например, мы говорим о торможении автомобиля. В чисто резаном повороте происходит срезание и удаление из карвингового следа части снега, а также некоторая деформация снега, вследствие его уплотнения под действием скользящей поверхности лыжи, когда происходит формирование резаного следа.
Современная профильная наука полагает, что при движении лыжи через данную точку склона снег в этой точке уплотняется и частично срезается при прохождении по нему первой половины лыжи. Глубина проникновения канта в склон в этой точке склона максимальна в момент прохождения середины лыжи. Вторая половина лыжи едет по готовой канавке (Федерольф (2005), Рейд (2010)).
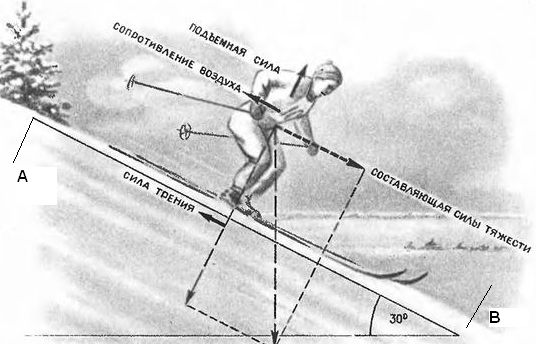
Здесь уместна аналогия с долинными лыжами, когда лыжник едет не по накатанной лыжне, а по мягкой трассе. При формировании лыжни лыжи уплотняют снег. Основное уплотнение снега происходит при прохождении первой половины лыжи. При этом первая половина лыжи изгибается и получается подобие наклонной плоскости, на которую давит деформируемый лыжей снег. Сила, с которой снег давит на переднююполовину лыжи, имеет составляющую, направленную против движения лыжника. 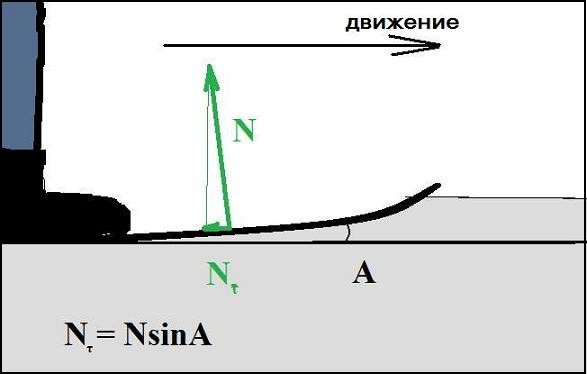Эта сила и мешает движению лыжника (Рис2).
Рис.2
Направление скользящей поверхности первой половины лыжи составляет небольшой угол А с направлением движения, поэтому сила реакции уплотняемого снега Ν направлена НЕ вертикально и имеет составляющую Ντ, направленную против движения лыжника. Эта составляющая силы реакции опоры Ντ и является «дополнительной силой трения», но, очевидно, что это - НЕ трение в обычном понимании.
Когда лыжа движется по активной дуге резаного поворота, то при формировании резаного следа действует примерно такой же механизм, как и при формировании лыжни долинных лыж.
Повторю. Носок поставленной на кант лыжи начинает формировать резаный след на поверхности склона в некоторой точке. При дальнейшем движении канта лыжи через данную точку след углубляется, достигая максимальной глубины при прохождении через эту точку середины канта. Вторая половина канта движется уже по готовому следу (Федерольф (2005), Рейд (2010)).
В работе (Lieu&Mott 1985) , было отмечено, что даже при установившемся режиме карвинга все точки передней части лыжи движутся также как и в режиме проскальзывания (skidding) - «по своим собственным траекториям», то есть по траекториям, отличным от траектории движения центра и задней части лыжи. Передняя часть лыжи больше деформирована, она изогнута сильнее, чем задняя часть лыжи.
Передняя часть лыжи движется под некоторым углом к траектории движения центра лыжи и ее задней части в полной аналогии с движением передней части долинной лыжи при формировании ею лыжни (Рис.2). Это хорошо видно на схеме (Рис.3), приведенной в работе (Рейд 2010) со ссылкой на работу (Lieu&Mott 1985)
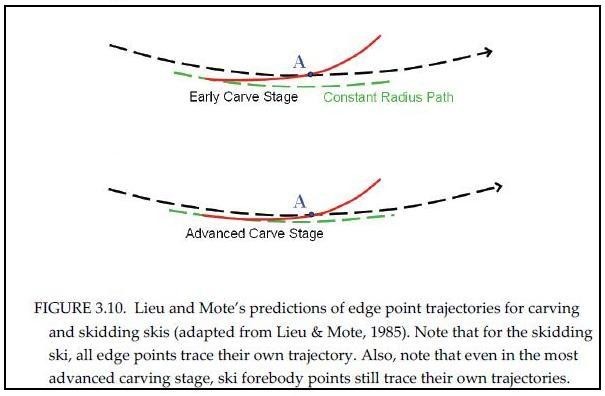
Рис. 3 Схема из работы (Рейд 2010), показывающая переход лыжи от стадии проскальзывания к стадии развитого карвинга.
Приведу замедленное видео (Рис3.1(а,б)), иллюстрируещее идею и схему (Lieu&Mott 1985). На видео Рис.3.1(а) можно видеть на сколько широк чистый карвинговый след, оставленный лыжником при предыдущем проезде мимо камеры (левая часть кадра).
Рис. 3.1(а)Как формируется карвинговый след можно видеть на этом замедленном видео Д. Куше. Хорошо видно сильный иизгиб передней половины лыж, ширину следа и то, что носы лыж находятся все время на поверхности склона
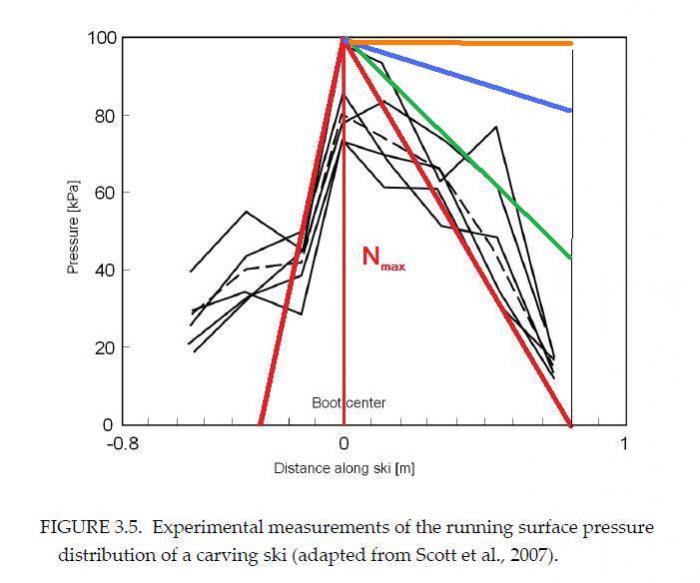
Рис.3.1(б)Совершенно очевидно, что на переднюю часть лыжи со стороны склона действует гораздо бОльшая сила, чем на ее заднюю часть. Существуют многочисленные модели распределения давления со стороны склона на лыжу вдоль длины этой лыжи. Одна из таких численных моделе представлена на Рис. 4(а). Имеются даже чисто экспериментальные данные по распределению давления со стороны склона на лыжу вдоль длины этой лыжи (Рис.4(б))
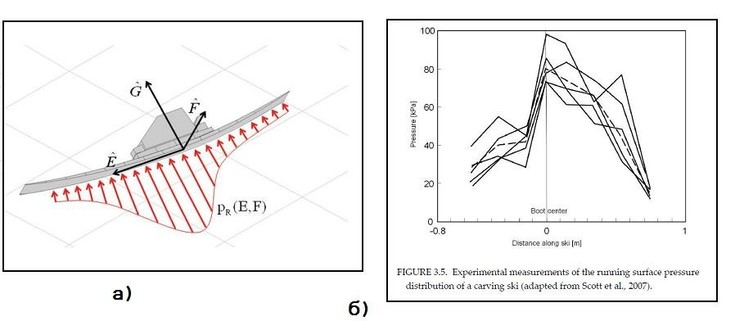
Рис.4 Теоретическое (а) и экспериментальное (б) распределение давления, действующее со стороны склона на лыжу движущуюся в дуге резаного поворота. Схемы адаптированы из работы (Рейд 2010).
Теперь у нас есть вся информация для того, чтобы вычислить составляющую силы реакции склона, действующую на режущую дугу лыжу против движения центра этой лыжи и замедляющую это движение. Это можно сделать точно также, как я это сделал для случая долинной лыжи при вычислении «дополнительной силы трения» Ντ (Рис.2) Результат этих вычислений позволит ответить на вопрос из заголовка данной статьи.
Для начала следует определить, насколько сильно радиус изгиба передней части режущей дугу лыжи отличается от радиуса резаного поворота, который, как следует из Рис. 3, равен радиусу изгиба задней части лыжи.
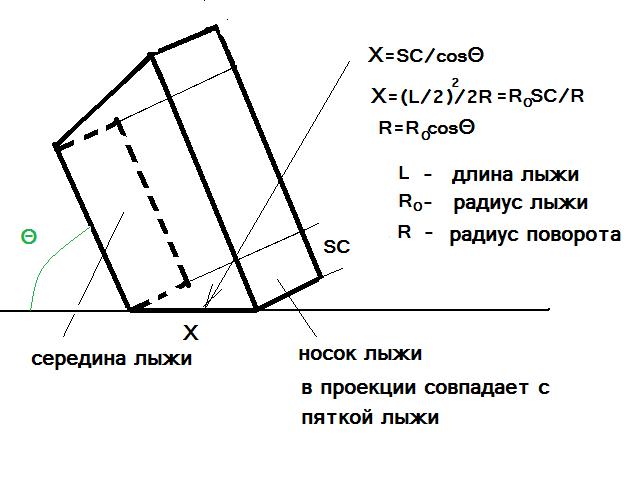
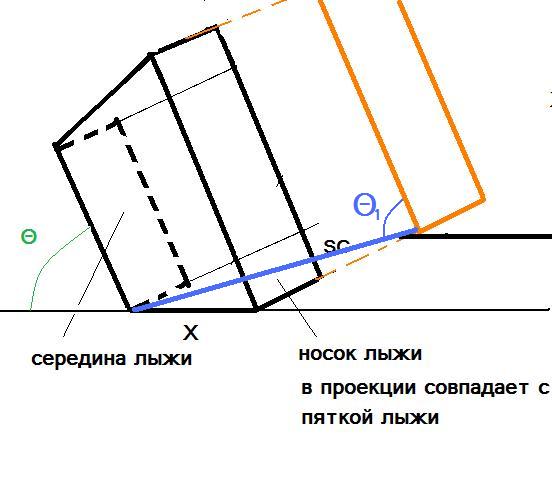
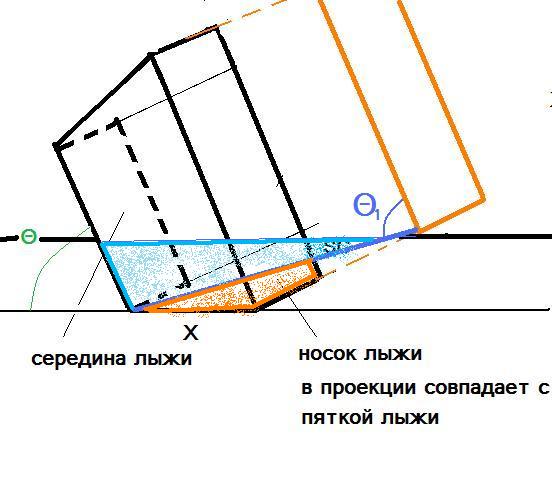
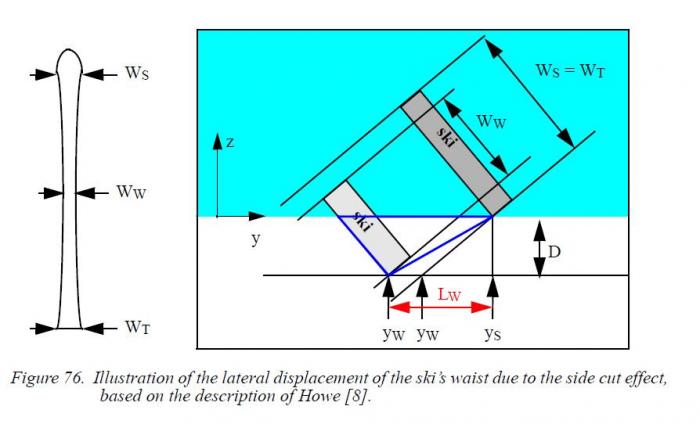
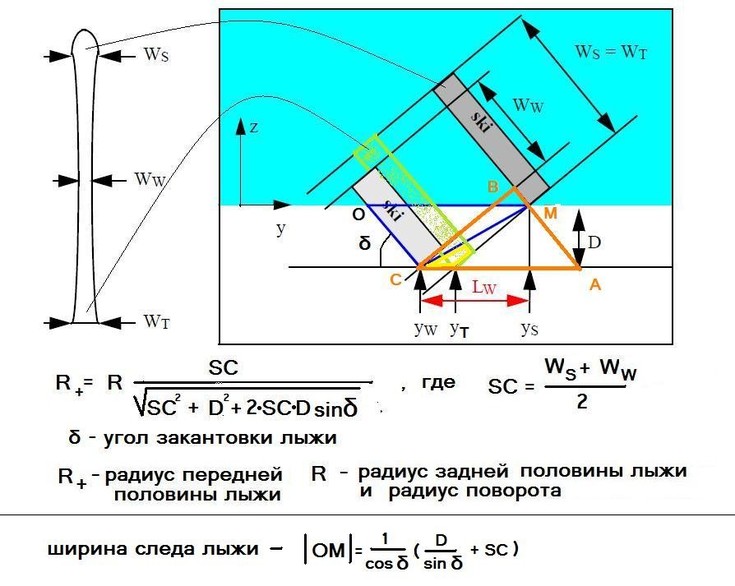
Воспользуемся схемой из работы (Федерольф (2005)) (Рис.5), изображающую процесс формирования резаного следа. В эту схему мной добавлено изображение задника лыжи (зеленый прямоугольник) и необходимые вычисления и пояснения. Формула для радиуса передней части лыжи R+ вычисляется из сопоставления треугольников ABC и AMC.
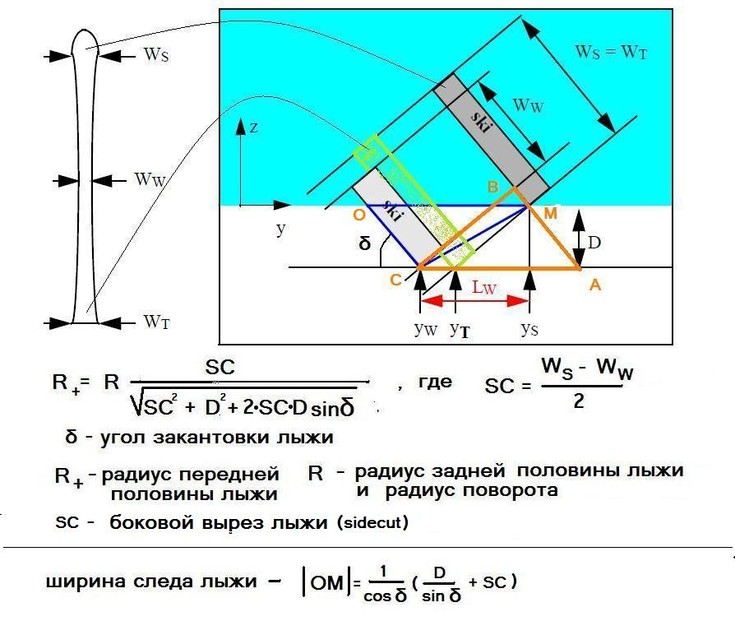
Рис. 5 Схема формирования резаного следа при чистом карвинге. Адаптирована из работы (Федерольф (2005))
Схема сложная для восприятия и требует пояснений. На схеме в несколько утрированном виде изображен вид спереди (против хода движения) на режущую склон лыжу. Белым цветом обозначен склон, синим - воздух. Лыжа изображена на схеме в виде трех прямоугольников - это сечения носка лыжи(большой серый прямоугольник), середины лыжи(большой зеленый прямоугольник) и пятки лыжи(малый серый прямоугольник). Даны их положения (ys yw yT соответственно), их размеры (WsWwWT соответственно) и показаны соответствующие им места на изображении лыжи (слева на рис.5).
Передняя часть лыжи при движении вырезает в склоне канавку треугольной формы, сечение которой на схеме обозначено синим треугольником ОМС. В итоге след лыжи получается треугольной формы, которая ясна из Рис.5.
На Рис. 5.1 приведен вид сверху на режущий кант лыжи, которая изображена на диаграмме Рис.5 с соответствующим обозначением характерных точек канта.
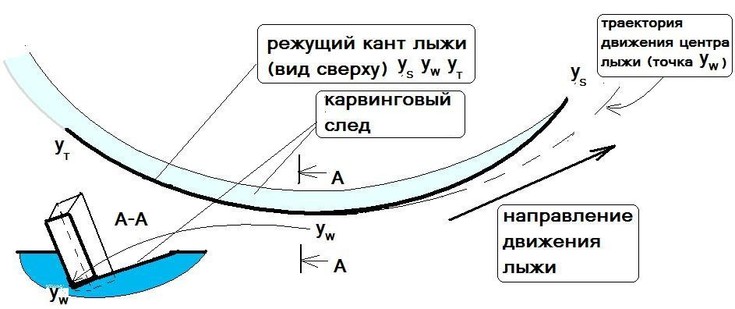
Рис 5.1 Схема формирования следа лыжи при чистом карвинге (вид сверху).
При больших углах закантовки лыжи, когда синус угла закантовки близок к единице, формула для определения радиуса передней части лыжи R+ (Рис.5) приобретает совсем простой вид.
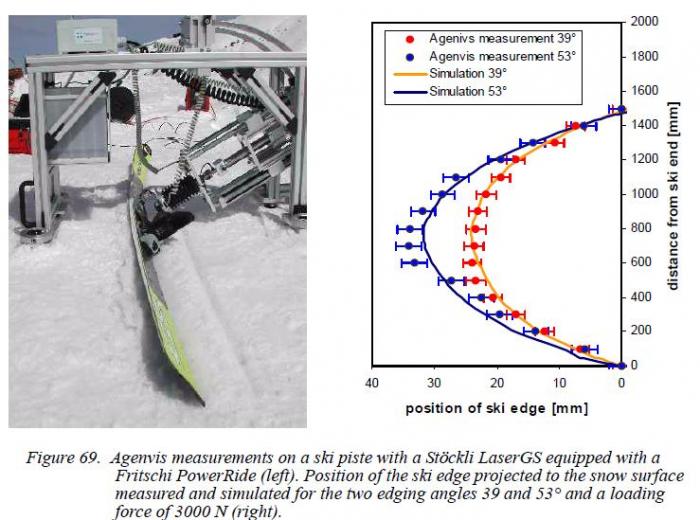
Приведу данные по глубинам следа лыжи из работы (Федерольф (2005)) (Рис. 5.2)
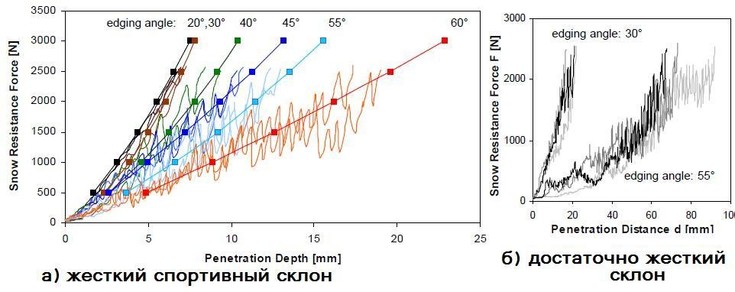
Рис 5.2 Экспериментальные и расчетные данные по глубинам следа лыжи для склонов различной жесткости из работы (Федерольф (2005))
Так как величина SC сравнима с глубиной резаного следа D, а для мягкого склона может быть и меньше этой глубины, то величина радиуса передней части лыжи может в разы отличаться от радиуса задней части лыжи. Например, величина бокового выреза слаломных лыж, которые использовали спортсмены для тестовых проездов в исследовании (Рейд(2010)) составляла 20мм.
Интересно, что ширина чистого карвингового следа (Рис. 5 и 5.1) при больших углах закантовки является достаточно большой величиной даже в случае достаточно жесткого (отратраченного) склона. Так, для следа лыжи глубиной 40мм (на Рис. 5.2 (б) для угла закантовки лыжи в 600 этому значению глубины следа (Penetration Depth) соответствует Penetration Disnans в 80мм) даже при относительно небольших углах закантовки в 55-600 достижимых в коротком резаном повороте, ширина следа лыжи будет превышать 14 см.
Определим теперь «дополнительную силу трения» Ντ для режущей активную дугу лыжи. Для этого аппроксимируем экспериментальные данные (Рис.4(б)) по распределению давления со стороны склона на лыжу вдоль длины этой лыжи линейной функцией (Рис.5).
Для вычислений понадобится только ТИП кривой распределения давления по длине лыжи. Величина пика нагрузки (на схеме - Nmax ) зависит от конкретной величины ЦБС, которая действует на лыжника в повороте в данный момент и будет определена при дальнейших вычислениях.
Необходимо отметить, что для для более жестких лыж эпюра давления будет менее "скошена" в носку лыжи. Чем жестче будут лыжи, тем равномернее будет распределяться давление по первой половине лыж.
Как покажут дальнейшие вычисления даже такой простой аппроксимации (Рис.6) вполне достаточно для получения достаточно точного результата, так как механизм контроля скорости в резаном повороте определяется в основном тем, что радиус передней части лыжи сильно отличается от радиуса задней части лыжи.
Рис.6 Красным цветом показан ТИП эпюры распределения давления по длине лыжи, который используется в данной статье для вычислений.
Теперь можно вычислить составляющую силы реакции опоры параллельную поверхности склона, а затем определить уже ее составляющую, которая действует на лыжи как «дополнительная сила трения». Чтобы не загромождать статью формулами я привожу на Рис.6 достаточно утрированную схему, на которой изображена очень сильно изогнутая лыжа. На схеме также приведены приближенные вычисления, использующие то обстоятельство, что угол закантовки лыжи достаточно большой, а длина лыжи мала по сравнению с радиусом поворота.
Рис. 7
Теперь нужно вспомнить, что для больших углов закантовки величина Nn с достаточно большой точностью равна величине ЦБС плюс/минус величина проекции ускорения ЦМ лыжника на линию О-ЦМ, умноженную на массу лыжника. Это приближение выполняется даже для случая динамического резаного поворота.
Используя результаты, полученные в этой статье и отображенные на рисунках 5 и 7, и учитывая, что нормальная к склону составляющая силы реакции опоры так же дает свой вклад в «дополнительную силу трения», получаем для величины «дополнительной силы трения» при больших углах закантовки лыжи следующее приближенное соотношение:
Рис. 8
Я намеренно привел это приближенное выражение для величины «дополнительной силы трения», которое является достаточно точным для больших углов закантовки лыж, так как из него непосредственно следует, то, каким образом лыжник может регулировать величину эффективного коэффициента трения и контролировать скорость в резаном повороте. Так лыжник может менять расстояние между своим ЦМ и лыжами - О-ЦМ с соответствующими ускорениями и тем изменять величину давления, которое лыжник оказывает на лыжу и, соответственно, изменять величину «дополнительной силы трения». Причем глубина резаного следа D также линейно зависит от величины давления, которое оказывает лыжник на лыжу (Рис5.2).
По поводу коэффициента 1/3 необходимо отметить, что для более жестких лыж этот коэффициент становится немного больше и в пределе стремиться к 1/2.
Точность этого выражения можно проверить, используя фактические данные по проездам спортсменов, которые имеются в профильной литературе. Так для данных, приведенных на Рис. 1(б) из работы Рейда (2010) указано, что минимальный радиус траектории поворота слаломиста в момент, когда ускорение его ЦМ было 4м/с2 а скорость – 12.1м/с (красная точка на Рис 1(б)) составлял составлял 3.96 м, длина слаломных лыж 1.65м . Величина силы реакции склона превышала в 3-3.5 раза вес лыжника в покое. Подставляя все эти данные в полученное выражение, считаем, что лыжник поддерживает расстояние О-ЦМ постоянным, то есть "упирается в лыжу" и получаем, без учета сомножителя, содержащего глубину следа лыж, 2.58м/с2 .
Сомножитель, содержащий глубину следа лыж, является величиной большей 1 и для глубины следа в 20мм он будет равен 2, а для глубины 30мм он будет равен 2.5, так как величина бокового выреза лыж в данном случае равна 20мм.
Таким образом действие «дополнительной силы трения» обеспечивает замедление ЦМ этого слаломиста в апексе поворота величиной в 5.16– 6.45 м/с2. Учитывая, что величина скатывающей силы в этот момент обеспечивает ускорение ЦМ лыжника величиной примерно 2.5 м/с2 , а "обычная" сила трения обеспечивала торможение величиной примерно 0.6-0.7 м/с2 , получаем «чистое» замедление лыжника в апексе дуги величиной 3.3 - 4.6м/с2. Величина этого замедления измеренная экспериментально составляет 4м/с2 , что достаточно хорошо соответствует теоретической оценке.
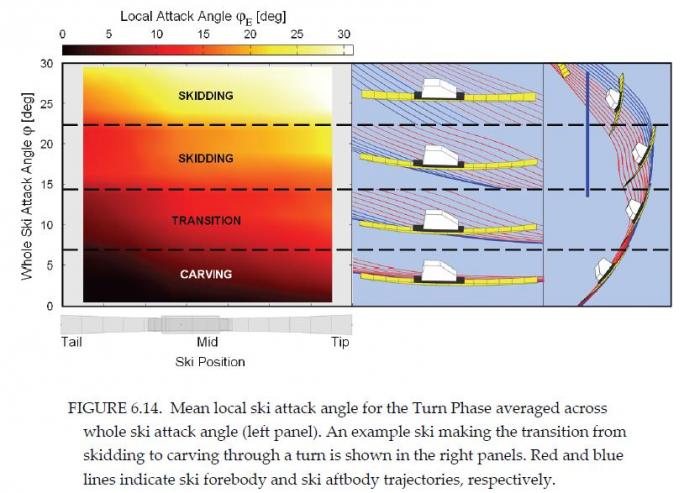
Можно оценить так называемый угол атаки лыжи, а именно угол между направлением продольной оси лыжи и направлением скорости ее центра. Этот угол ς в рассмотренной модели возникает из-за того, что передняя часть лыжи изогнута больше, чем задняя половина лыжи, которая едет точно по карвинговому следу (Рис. 9).
Оценка этого угла дает в апексе поворота примерно 0.12рад = 6-70 для глубины следа 20мм
Рис.9
У Рейда (2010) он называется "угол атаки" и он был экспериментально измерен. Значения в апексе составило примерно 5-60 (Рис.10)
Рис.10
Таким образом модельочень хорошо количественно согласуется с фактическими данными, измеренными экспериментально.
Из полученного выражения (Рис.8) видно, что эффективный контроль скорости при карвинге возможен только в случае использования лыжником достаточно больших углов закантовки лыж в апексе поворота.
Также видно, что величина «дополнительной силы трения», при больших углах закантовки и прочих равных условиях, линейно зависит от глубины резаного следа лыж, поэтому совершая действия, которые приводят к бОльшей загрузке лыж и особенно в направлении нормали к склону, лыжник увеличивает глубину резаного следа и, соответственно, увеличивает эффективный коэффициент трения.
Глубина резаного следа лыж зависит как от величины, так и от направления действия силы, с которой лыжник загружает лыжи. Чем ближе линия действия этой силы к биссектрисе режущего канта, тем на большую глубину будет проникать в склон лыжа при одинаковой величине ее загрузки лыжником.
В немалой степени, такие действия связаны с правильным применением лыжником такого технического приема как движение по созданию "углового положения" своего тела (ангуляция) (Рис.9). Такое движение при правильном выполнении приводит к существенному изменению как величины так и направления загрузки лыж.
В англоязычной литературе эту группу технических действий связывают с терминами «counteracting» и «counterbalancing». Однако, в профильной литературе отсутствует понимание физического механизма действия этих приемов на загрузку лыж, поэтому нет четких рекомендаций о том, что именно является правильным и существенным при выполнении этой группы технических действий.
Здесь необходимо заметить, что лыжник своими активными дествиями должен ДОПОЛНИТЕЛЬНО загружать лыжи в направлении «к склону» , лежащем в плоскости скользящей поверхности лыж (на Рис. 11 это направление показано красными стрелками), так как в направлении " вдоль плоскости склона" лыжи и так сильно загружены действием ЦБС.
Рис. 11
Некоторые действия, которые традиционно рекомендуют применять для загрузки носков лыж оказываются бесполезными и даже вредными в случае когда лыжи сильно закантованы. Например, простой перенос давления на носки лыж путем подачи корпуса «вперед» является для контроля скорости в дуге не только бессмысленным действием, но и может привести к срыву лыж из-за перегрузки их в плоскости склона.
Чтобы увеличить среднее давление на лыжи в направлении склона в активной дуге поворота лыжнику следует увеличить стадию безопорного транзита между активными дугами. Я рассматривал этот вопрос в статье «Что должен делать лыжник чтобы его лыжи надежно резали склон.»
Для загрузки лыж в нужном направлении (Рис.9) лыжнику следует использовать инерцию вращения своего тела вокруг своей главной вертикальной оси инерции. Один из таких приемов, который применяется в начале активной дуги поворота, был рассмотрен в статье «Ключ к технике резаного поворота».
Следует отметить, что, находясь в активной дуге, лыжник вполне способен своими активными действиями достаточно быстро и существенным образом влиять на степень загрузки лыж в направлении нормали к склону и тем самым оказывать сильное влияние на величину «дополнительной силы трения», как увеличивая ее, так и уменьшая. Некоторые такие действия будут рассмотрены мной в следующих статьях.
Выводы:
0) Само по себе чистое резаное ведение лыжи на оптимальной скорости в активной дуге поворота содержит механизм контроля скорости движения лыжника, что позволяет лыжнику эффективно контролировать величину скорости спуска путем использования достаточных по величине углов закантовки лыж в апексе поворота и активных действий амортизационного типа и типа «counterbalancing». Увеличение лыжником угла закантовки лыж в апексе поворота усиливает динамику поворота в целом, что увеличивает давление лыж на склон в апексе поворота и приводит к общему углублению следа лыж в активной дуге в целом и в апексе поворота в частности. Применение лыжником достаточно активных действий действий амортизационного типа и типа «counterbalancing» приводит к увеличению в том числе и нормальной составляющей силы давления лыж на склон и к сооветствующему увеличению глубины следа лыж в активной дуге поворота. Увеличение как угла закантовки лыж в апексе поворота, так и глубины следа лыж в активной дуге поворота, приводит к существенному увеличению эффективной силы трения, связанной с деформацией снега при формировании чистого карвингового следа.1) В идеальном резаный повороте (чистый карвинг) происходит НЕИЗБЕЖНОЕ и достаточно сильное торможение лыжника при его движении даже по идеальной карвинговой дуге. Высококласные спортсмены при ШТАТНОМ прохождении спортивной трассы ТОРМОЗЯТ в каждой активной резаной дуге со скоростью, которая может значительно превышать скорость торможения автомобиля на сухом асфальте.
2) Процесс чистого карвинга характеризуется тем, что лыжа в каждый момент движения вырезает на поверхности склона канавку примерно треугольного сечения. Основную работу совершает передняя половина лыжи, которая вырезает канавку треугольной формы (синий треугольник на Рис.5). Задняя половина лыжи движется ужепо готовой канавке. Глубина канавки достаточна для того, чтобы нагрузка на склон не превышала предел прочности снега на сдвиг. Но, так как канавка вырезается, и снег из нее удаляется, то на это требуется затраты кинетической энергии лыжника, что приводит к замедлению движения лыжника при выполнении им идеально чистого резаного (карвингового) поворота.
2) При формировании следа лыж (канавки) в чистом резаном повороте, вследствие смещения слоев снега и его неминуемого удаления из канавки, возникает соответствующая сила реакции склона, одна из компонент которой компенсирует действие центробежной силы и удерживает лыжи от проскальзывания их поперек траектории их движения, тогда как другая компонента этой силы направлена против движения лыжника. Именно она замедляет скорость лыжника при чистом карвинге.
3) Величина замедляющей движение лыжника силы (пункт 2) при больших углах закантовки лыж прямо пропорциональна квадрату скорости движения лыжника, глубине оставляемого лыжами следа и длине лыж. Эта величина обратно пропорциональна квадрату радиуса поворота лыжника (Рис.8)
4) Если у лыжника не получается контролировать скорость в резаном повороте и ему приходится для контроля скорости применять приемы типа "сброс пяток", то это не значит, что контроль скорости в резаном повороте без таких приемов (типа "сброса пяток") невозможен, просто в технике лыжника имеются существенные недостатки.
5) Если лыжник хочет ездить чисто резаным поворотом, то ему необходимо освоить группу движений, которые способствуют БЫСТРОЙ загрузке лыж в направлении "вдоль плоскости скользячки к склону" (на Рис. 9 это направление показано красными стрелками). Дополнительная загрузка лыжи именно в этом направлении наиболее эффективно приводит к увеличению глубины следа лыжи и соответствующему увеличению "дополнительной силы трения." Также загрузка лыжи именно в этом направлении с наибольшей эфективностью передается носку лыжи, так как в направлении плоскости скользячки лыжу можно считать абсолютно жесткой, тогда как в поперечном плоскости скользячки направлении лыжа достаточно легко изгибается.
6) Ширина чистого карвингового следа (рис.5) при больших углах закантовки является достаточно большой величиной даже в случае достаточно жесткого (отратраченного) склона. Так, для следа лыжи глубиной 40мм (Рис. 5.1) даже при относительно небольших углах закантовки в 55-600 достижимых в коротком резаном повороте, ширина следа лыжи будет превышать 14 см. При этом с каждого пройденного метра траектории из под лыж будет "вылетать" до 5-6 л (по объему) снега.
Подробные ссылки на источники, упомянутые в данной статье содержатся в библиографиях к диссертационным работам Р. Рейда (2010) и Федерольфа (2005)
"A kinematic and kinetic study of alpine skiing technique in slalom" Reid, Robert C. (Doctoral thesis, 2010)
"Finite Element Simulation of a Carving Snow Ski" Federolf, Peter Andreas (Doctoral thesis, 2005)
Зато Дао-карвинг возможен 
(ну теоретически обосновал)
вызывает вопрос: почему «дополнительная сила трения» не равна нулю при нулевой канавке D=0? Выходит, если потерь энергии нет вовсе, то торможение все равно происходит?
