Карвинговая лыжа. В поисках идеала

Хотя настоящая статья готовилась автором как самостоятельная, но появление в "лыжном информационном пространстве" материалов пересекающейся тематики позволяет автору квалифицировать её, как отклик на эти публикации. Имеются в виду статьи Александра Ревкуса "Зависимость между углом закантовки и радиусом поворота лыжи" и Александра Каниовского Некоторые аспекты карвингового поворота.

Это предоставляет автору возможность не возиться с определениями и терминами, отсылая всех к указанным источникам, чем он с удовольствием и воспользуется.

В целом, в творчестве указанных авторов присутствует нездоровый мотив очернения последних достижений зарубежного лыжестроения, представленных лыжами карвинговой геометрии. Исходя из туманных посылок и используя изощрённые формулы, иррациональные числа и трансцендентные функции, что практически граничит с метафизикой, они пытаются убедить нас, что апофеоз лыжетворения - карвинговый чистый резаный поворот, не является таким уж идеалом, а имеет отдельно взятые недостатки, на которые, впрочем, при умелом использовании лыжи, можно закрыть глаза.

В намеренья автора не входит опровергать выводы данных статей. Напротив, он намерен показать, что на самом деле в смысле идеала всё гораздо хуже. После долгих раздумий он решил назвать статью так, как она названа, поскольку у каждого из авторов эта тенденция, так или иначе, прослеживается. Заметь, читатель, - такое название как бы возвышает всех авторов над суетой лыжных буден и придаёт им некий ореол романтических борцов за нашу, лыжную правду. Что касается эпиграфа, а, как заметил автор, в последнее время они опять вошли в моду, то над ним автор долго не задумывался. Поэтому возможна некоторая неоднозначность его толкования, что, впрочем, свойственно всем эпиграфам.

Нате!
В.Маяковский

Как, вероятно, и большинство из нас, автор долгое время внимал сладкоречивым песням о неоспоримых достоинствах и прелестях "чистого" резаного ведения , "ведения поворота без малейшего проскальзывания" и прочим подобным вещам, как изустно, так и в печатном виде. Наблюдая развалы лыж новой, причём самой разнообразной, геометрии, каждая из которых претендовала на звание идеала, автор никак не мог взять в голову, - один ли это идеал или же все разные? На этой почве у автора развился доминантный интерес, возможно, нездоровый, к тому, что же должна представлять собой "идеальная" карвинговая лыжа. К чему он пришёл, он и намерен изложить читателю, по пути затронув, так или иначе, и результаты указанных работ. Поэтому добро пожаловать, читатель, в волшебный мир поисков идеала!

Для совершения таинства нам понадобятся три вещи:

• лыжи, способные резать дугу поворота,
• лыжник, способный оказать им в этом хоть какую-нибудь помощь,
• снег, способный всё это терпеть.

Не будет преувеличением сказать, что в дальнейшем наличие этих вещей будет предполагаться.

Указанный жанр статьи позволяет автору обойтись без описания того, что такое резаный поворот, поэтому он ограничится кратким резюмированием:

• загруженная лыжа прогибается по дуге, которая определяет радиус поворота;
• прогиб лыжи определяется формой бокового выреза и величиной угла закантовки;

Чуть ниже эти понятия будут несколько уточнены.

Анализируя зависимость радиуса поворота лыжи от угла закантовки и А. Каниовский и А. Ревкус, исходя из разных посылок, впали в один общий грех, отталкиваясь от геометрии бокового выреза и приняв за основу поворота форму линии (подчёркнуто автором) прилежания канта. В результате у них лыжи перестали ездить прямо. Между тем, последовательность рассуждений, приводящая, по мнению автора, к правильной постановке задачи, несложна и справедлива для любого состояния снега, в котором только возможен резаный поворот.

• Лыжа, как и всё, всё, всё, поворачивает под действием некоторых сил;
• Силы эти образуются в результате взаимодействия лыжи со снегом;
• Взаимодействовать со снегом может только поверхность лыжи; линия же, как нечто, не имеющее ни ширины, ни высоты, ни с чем взаимодействовать не может;
• Из поверхностей лыжи в данном контексте присутствуют две: скользящая и боковая. Если скользящая поверхность претендует на "руководящую" роль в повороте, то роль боковой поверхности в резаном повороте пока не ясна, но, как увидит далее читатель, она тоже заслуживает внимания;
• Лыжа в повороте, находясь, с одной стороны, под действием силы давления со стороны лыжника, сосредоточенной в районе грузовой площадки, и силы давления со стороны снега, распределённой по длине канта, прогибается в соответствии со своими жесткостными характеристиками до тех пор, пока не займёт устойчивое положение с опорой о снег.
• При этом её скользящая поверхность примет некоторую форму, отличную от исходной (для простоты будем считать, что исходная форма для неё - плоскость). Именно форма скользящей поверхности лыжи, а, точнее, форма её сечения плоскостью склона, а, ещё точнее, формы всех её подобных сечений для той части скользящей поверхности, которая взаимодействует со снегом, и будут определять радиус поворота лыжи.

В том, что это так, можно убедиться, проведя мысленный или же, при большом недоверии к своим умственным способностям, натурный эксперимент. Представим себе лыжу "сверхкарвинговой" геометрии, которая не приталена, а имеет в плане, наоборот, бочкообразную форму. Давайте прогнем её (а доля этого нам придётся воспользоваться подручными материалами, например, верёвкой, изобразив нечто вроде лука) и попробуем прокатиться на ней. Если закрыть глаза на форму боковой поверхности (автор предупреждал), то на ней вполне можно совершать резаные повороты. Если же кого-то всё же смущает боковая поверхность, то можно свести её роль к минимуму, взяв очень тонкую лыжу или заменив её полотном от двуручной пилы, сточив с него предварительно зубья для чистоты эксперимента. Так вот, она поедет именно в соответствии с формой скользящей поверхности.

Из этого несложного рассуждения следует также и роль бокового выреза "нормальной" карвинговой лыжи - он предназначен именно для формирования, в прямом смысле этого слова, скользящей поверхности лыжи. Вопрос может стоять только о соответствии или несоответствии его и формы скользящей поверхности в деформированном состоянии лыжи.

Отсюда же можно заметить, что боковая поверхность лыжи тоже на что-то влияет. По умолчанию обычно принимается, что, в деформированном состоянии лыжи, боковая поверхность наружным краем канта касается плоскости склона и также становится плоской. Но идеального ничего не бывает. А если она в этом состоянии слегка выпуклая или слегка вогнутая? Как это влияет на поведение лыжи при больших углах закантовки, особенно при тех условиях нагружения, о которых пойдёт речь ниже? В этом смысле автор хочет лишь отметить, что в условиях поворота с проскальзыванием подобные вопросы не возникали вообще.

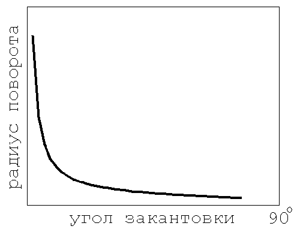
Как, наверное, уже заметил вдумчивый читатель, а других автор и не предполагает, при изложенной постановке вопроса о радиусе поворота как-то резко пропадает желание что-нибудь быстро посчитать. И автор в этом смысле не исключение. Просто, рассуждая логически, он пришёл к выводу, что, коли скользящая поверхность лыжи по мере увеличения угла кантования плавно деформируется начиная от плоского своего состояния, то и радиус поворота изменяется от плоского состояния, то есть от бесконечности. По представлениям автора, зависимость радиуса поворота от угла кантования имеет примерно следующий вид. Автора мало интересуют цифры, скорее, - закономерности.. Тем более, что для дальнейших рассуждений достаточно, что такая зависимость существует и она однозначна.

Дополним вышеперечисленные условия резаного поворота ещё и условием нагружения лыжи. Оно подразумевает, что лыжа должна быть закантована так, чтобы линия действия силы, с которой лыжник давит на лыжу, была перпендикулярна её скользящей поверхности. Если угол между линией действия силы и скользящей поверхностью, измеренный в поперечной плоскости с наружной стороны поворота, больше 90 градусов, то лыжу, как и всякое тело, находящееся на наклонной плоскости, начнёт выпирать из канавки, ею образованной, что приведёт к срыву резаного ведения. Если этот угол меньше 90 градусов, то, наоборот, лыжу начнёт вдавливать в канавку, что тоже не подарок. Во всяком случае, это увеличит врезание канта и, соответственно, сопротивление. И увеличит давление на боковую поверхность лыжи. Так что 90 градусов будет самое то.

Напомним читателю, что Рон Ле-Мастер в книге "На кантах", обессмертившей его имя, называл условие нагружения "критическим углом кантования" , имея в виду тот самый угол, о котором только что шла речь. Чтобы избежать путаницы с углом кантования в его обычном понимании, автор предпочитает называть это так.

Отметим, что в работе А. Каниовского это условие присутствует, хотя и не сформулировано явно. В статье А. Ревкуса оно обеспечивается, видимо, по замыслу автора, за счёт жесткости "каркаса" "лыжник-лыжа" .

В этом месте автор хотел бы выразить признательность читателю, который сумел прочитать все эти скучные и малополезные вещи, и заверить его, что дальше будет немного веселее.

Для развлечения давайте решим вопрос - будут ли проскальзывать лыжи у лыжника, совершающего прямой спуск вниз по склону? А чтобы развлекались не на счёт автора, он сразу добавляет: если лыжи у лыжника не плоские, а, вследствие ли стихийных бедствий, происков производителя или другого форс-мажора, имеют некоторую, отличную от плоскости, скользящую поверхность, например, винтовую. Честно говоря, автор и сам не знает, что из этого получится, но предполагает, что, в общем случае, лыжи будет уводить в сторону, или в разные стороны. Лыжнику придётся прикладывать к ним некоторые усилия, чтобы направить на "путь истинный" . В результате и возникнет проскальзывание и торможение. Из этого маленького умозаключения можно сделать также маленький, но полезный вывод: скользящая поверхность лыжи должна соответствовать той поверхности, по которой она едет.

Далее представим себе лыжника, совершающего на плоском склоне поворот самой простой формы - поворот по дуге окружности некоторого радиуса R и с некоторой скоростью V. Для этого лыжник должен выполнять много различных действий и движений, которые автору лень перечислять, и которые всем известны. Теперь давайте возьмём лопату у проезжающего мимо бордера и выкопаем или насыпем на нашем склоне поверхность такой формы, чтобы наш лыжник мог выполнить этот свой поворот с наименьшими "трудозатратами" . Такая поверхность - не новость, если вспомнить, как оформляются виражи на автомагистралях и желдорпутях. Применительно к лыжам её несложно представить, да нетрудно и нарисовать.

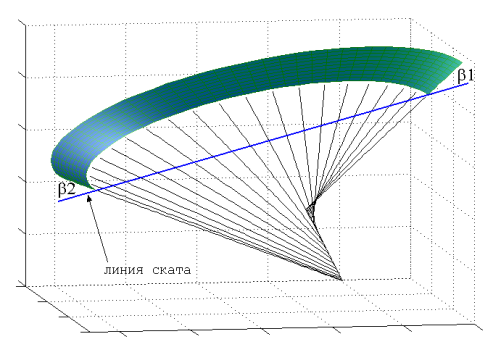
По определению это поверхность, которая в любой момент времени перпендикулярна линии действия суммарной силы, действующей на снег со стороны лыжника, или, наоборот, со стороны снега на лыжника. Любая из обсуждаемых статей содержит всё необходимое, чтобы рассчитать такую поверхность. Как видно из рисунка, поверхность нашего "специализированного" склона есть коническая поверхность с переменным углом раствора. В зависимости от сочетания радиуса поворота, скорости лыжника и угла падения склона эта поверхность будет как-то видоизменяться, но характер её останется одним и тем же Например, при изменении скорости при том же радиусе поворота будут изменяться углы наклона этой поверхности к плоскости склона. Изменение угла раствора отражает также всемирно известный факт изменения величины и направления суммарной силы, действующей на снег со стороны лыжника, в зависимости от фазы поворота. Так что ничего нового автор не изобрёл. Но, взгляните, до чего же легко и удобно лыжнику катиться по такому склону! Ему же ничего делать не надо, - никаких тебе закантовок, ангуляций-триангуляций, лыжи прогибаются по склону и весело катят вниз в полном соответствии с условиями нагружения. Единственное, что нужно делать лыжнику, - это стоять на ногах и сохранять перпендикулярность к склону, что, в этих замечательных условиях уже тавтология. Естественно, что у автора сразу возникло желание принять поворот, совершаемый на таком склоне, за идеальный . По крайней мере, до тех пор, пока не будет предложено что-нибудь лучшее. Тогда дело осталось за малым,- необходимо, чтобы лыжа также соответствовала этому склону в каждой его точке. К тому же, заставить лыжника взять лопату и откопать такой склон - дело весьма проблематичное, и лыже придётся самой его формировать. Если это у неё получится, то это и будет "идеальная" лыжа. Как только мы примем это положение, мы можем сразу сформулировать некоторые требования к идеальной лыже: для всех рабочих углов закантовки.

• скользящая поверхность лыжи должна иметь форму конической поверхности;
• линия прилежания канта должна существовать.

Что касается первого требования, то можно сказать, что коническая поверхность полностью удовлетворяет тому, что ранее было сказано применительно к радиусу поворота. Все сечения такой поверхности плоскостями, параллельными плоскости склона, есть дуги окружностей. Условие нагружения лыжи выполняется по определению. Все локальные углы закантовки для такой лыжи равны между собой.

Отметим небезынтересный факт, - коническая поверхность у лыжи может быть образована только за счёт её торсионного скручивания. Абсолютно жесткая в торсионном плане лыжа может деформироваться только в цилиндрическую поверхность. Для такой поверхности равенства локальных углов закантовки наблюдаться уже не будет.

Автор, слегка знакомый с конструкционными свойствами материалов, полагает, что получить идеальную коническую поверхность у лыжи можно только при тщательном, точнее, скурпулёзном подборе распределений продольной и торсионной жесткостей по длине лыжи и не менее тщательной подгонки формы бокового выреза (вспомним, для примера, хотя бы "3-D sidecut") для снега определённого состояния. И не упуская при этом из виду не менее важную задачу распределения давления по длине канта, которая также обеспечивается за счёт всё тех же характеристик. Поэтому автор выражает здоровое (большое) сомнение, что производителю удаётся обеспечить более ли менее идеальную форму лыжи во всём диапазоне рабочих прогибов лыжи. Скорее всего, она обеспечивается в узком диапазоне углов закантовки, рассчитанных на определённые условия использования и на определённый контингент.

Что же касается лыж с боковым вырезом в форме дуги окружности, то, если они и существуют, вероятно, изготавливаются для того же контингента, для которого Страдивари делал скрипки.

Отметим ещё, что А.Ревкус в своих изысканиях также опирался на конусную поверхность лыжи.

Второе условие отражает как раз соответствие между формой бокового выреза и формой скользящей поверхности. Понимать его следует так: если лыжу закантовать и прогнуть на жесткой плоскости, то линия канта должна касаться этой плоскости всеми своими точками.

Для получения более общей формулировки, приближенной к реальности, представим, что эта плоскость находится в глубине снежного покрова и лыжа на неё не опирается. Если линия канта так же целиком касается плоскости, то можно считать, что условие выполнено. Только сформулировать его придётся по-другому: линия канта должна быть кривой в плоскости, параллельной плоскости склона.

Из этих двух условий можно понаделать множество менее идеальных условий, приемлемых для того или иного состояния снежного покрова, но, поскольку нас интересует "идеальная" лыжа, мы этого делать не будем.

Теперь на такой лыже не грех и прокатиться. Обратимся снова к нарисованной "идеальной" поверхности. Предположим, что наша лыжа полностью соответствует начальной точке поворота, т.е. в загруженном состоянии ложится без зазора на эту поверхность. Тогда для той же лыжи, поставленной на нормальный склон, угол закантовки будет в точности равен углу наклона нашей идеальной поверхности к плоскости склона, и лыжа, закантованная на угол ß₁ при своём движении будет формировать в снегу именно такую поверхность. Сначала. Потом дело пойдет хуже. Как видно из рисунка, угол наклона идеальной поверхности постепенно увеличивается от ß₁ в начале поворота до ß₂ в конце поворота. Соответственно и лыжник должен увеличивать угол закантовки, поскольку это связано с поддержанием условия нагружения лыжи, и невыполнение его приведёт к срыву резаного поворота. Увеличение угла закантовки приведёт к уменьшению радиуса поворота, т.е. лыжник начнет съезжать с нашей идеальной поверхности внутрь поворота. Уменьшение радиуса поворота приведёт к увеличению центростремительной силы, что потребует от лыжника дополнительного увеличения угла закантовки для выполнения тех же условий. Дополнительное увеличение угла закантовки приведёт к дополнительному уменьшению радиуса и так далее? В результате либо сорвётся резаное ведение, либо лыжник вместо требуемой дуги окружности выпишет на снегу нечто вроде сворачивающейся спирали.

К таким же, примерно, выводам пришёл и А. Каниовский в результате "числового анализа" . Главное, считает он, вовремя спрыгнуть с этой спирали и начать новую, в другую сторону. Что ж, это тоже выход, но вот можно ли признать такой поворот удовлетворительным с точки зрения поиска идеала. Вряд ли. Поворот типа "куда кривая вывезет" вместо красивой дуги окружности как-то не вяжется с идеалом. К тому же, в пользу окружности, помимо эстетических, можно найти, наверное, и другие аргументы. Но мы этим здесь заниматься не будем, а посмотрим, можно ли совершить запланированный нами поворот как-нибудь иначе, например, на другой скорости.

Положим, что поворот того же радиуса R мы хотим совершить на нашей идеальной лыже, заточенной на этот радиус и скорость V, на скорости, меньшей, чем V. Вновь взглянем на нашу "идеальную" поверхность. Для меньшей скорости это будет уже другая поверхность, у которой угол и все прочие будут также меньше. И, если мы закантуем нашу лыжу на этот меньший угол, то получим, соответственно, больший радиус поворота, что нас не устраивает. Значит, мы должны закантовать лыжу именно на первоначальный угол ß₁, который обеспечивает требуемый радиус поворота. Но давайте посмотрим, что это означает.

Мы должны перекантовать лыжу, т.е. закантовать её на угол, больший, чем того требует условие нагружения. (автор использует курсив, чтобы, опять же, избежать путаницы с стандартным значением термина). Чем меньше скорость, тем на больший угол придётся перекантовать лыжи. Именно этот угол имеет в виду А. Ревкус, говоря о дополнительном угле закантовки и приводя различные цифры и диаграммы для его оценки.

Всё это звучит довольно безобидно, но вот как это воспринимается на уровне ощущений? Оденьте лыжи, станьте на пол и закантуйте их на сколько-нибудь значимый угол, сохранив при этом равновесие. Вот именно так и воспринимается. Если проделать это перед зеркалом (не будем сбрасывать со счетов и эстетический момент), то можно заметить явное сходство с бордером.

Но, тем не менее, такой поворот можно совершить при одном угле закантовки. Граничное значение скорости можно получить из условия равенства угла ß₂ для "малой" скорости и угла для скорости V, т.е. когда поворот начинается с некоторым нарушением условия нагружения, правда, не в худшую сторону, и заканчивается уже "идеально". Перекантовка, как уже говорилось, ведёт к дополнительному врезанию кантов. Можно ли принять такой поворот за "идеальный"? В той же степени, в какой можно принять за идеал прямой спуск в том положеиии, которое только что отразилось в зеркале.

Все промежуточные, между граничной скоростью и V, результаты будут просто комбинацией двух рассмотренных типов.

Со скоростью, большей, чем V, и совсем просто. Для неё угол ß₁ будет сразу больше, а радиус поворота меньше, т.е. это будет совсем другой поворот.

Таким образом, читатель, мы рассмотрели все возможные варианты исполнения резаного поворота, а "идеала" так и не нашли. То одно плохо, то другое. И все авторы были трогательно единодушны в качественной оценке особенностей резаного поворота. Это даёт нам право считать, что наши рассуждения не так уж и неверны. Поэтому автор берёт на себя смелость заявить: "чистого" или "идеального" резаного поворота не существует! И, прежде, чем вступать с ним в пререкания, давайте решим, - проблемы ли это резаного поворота или это проблемы нашего его осмысления. Обратимся к спортивной технике, которая должна являться и является, несомненно, передовым краем "резаного" фронта. Попытаемся объяснить себе те вещи, про которые не раз слышали и читали:

• почему резаный поворот исполняется с переменной (с носка на пятку) загрузкой лыжи?
• почему форма спортивного поворота напоминает разворачивающуюся спираль, тогда как она должна быть сворачивающейся?
• почему чистый резаный поворот сопровождается таким большим выбросом снега, как это видно, например, на иллюстрации к статье А.Каниовского?

Автор, увы, не знает ответов, и лишь робко рискует предположить: в силу "неидеальности". То ли лыж, то ли нашего "идеала".

На этой минорной ноте автор мог бы и закончить, но "идеала" мы так и не нашли, поэтому давайте напоследок бросим ещё ретроспективный взгляд в завтра. Как можно заметить, пристально рассматривая нашу "идеальную" поверхность, лыжа, которая бы ей соответствовала, должна иметь один и тот же радиус при изменении угла закантовки в разных фазах поворота. Практически это означает, что лыжа должна менять свои механические характеристики в ходе поворота. Ясно, что ни одна реальная лыжа этого делать не может, чем не напичкай её производитель. Пока. Но вот что обнадёживает, - изладили же дошлые ребята из К2 лыжи с "лампочками", над которыми долго измывалась рассылка RASC. А ведь пьезоэлемент - вещь обратимая. Изогни его - он выдаст напряжение, подай на него напряжение - он изогнётся. Чем же не средство активно управлять характеристиками лыжи. Что же мешает ребятам из К2 уклеить лыжу такими элементами, печатными проводниками, наставить сенсоров и контроллеров и формировать её по своему усмотрению, как душе угодно. Да ничего, как только они сообразят, как это делать. Поначалу, конечно, питание лыжи будут получать от "портативной" батареи, которую лыжник будет возить в маленьком изящном рюкзачке, как какой-нибудь... (тьфу, опять бордер попутал). Потом они научатся перераспределять энергию от пассивных элементов к активным, и тогда эту лыжу и не отличишь по виду от нынешних. Нет, лавинный датчик там, конечно, будет. За сотовый автор не скажет, но жаль дать пропасть такой антенне, как канты.

Кто знает, может уже сейчас в тайных лабораториях К2 куётся это новое и смертельное для конкурентов оружие, и мы все сможем скоро его увидеть. А те, у кого на это хватит денег - и покататься. Вот тогда мы и вернёмся к разговору об идеале.