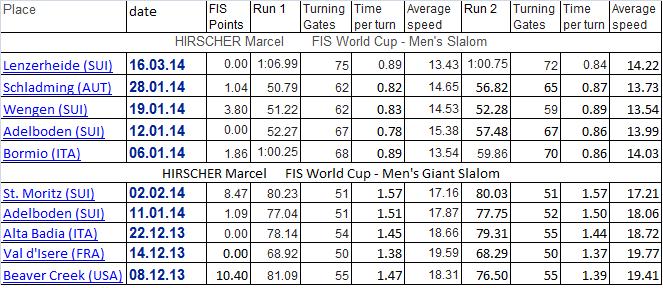
А действительно, почему? На сайте ФИС я взял данные о пяти последних выступлениях Марселя Хиршера в специальном слаломе (Slalom) и гигантском слаломе (Giant slalom) на Кубке мира 2013-14 года. Результат получился неожиданным и парадоксальным.
Вот что получилось по официальным данным опубликованным на сайте ФИС (для расчета средней скорости принято, что расстояние между воротами в слаломе - 12м, в ГС - 27м)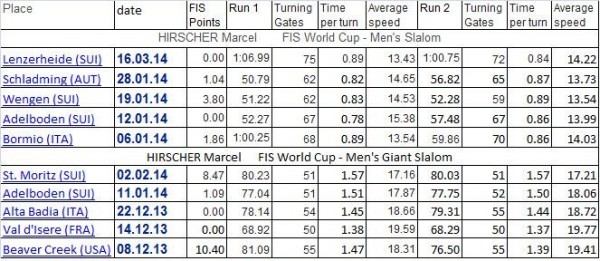
Хиршер - слаломист проигрывает в скорости Хиршеру - гигантисту. Причем скорсть движения Хиршера по трассе слалома и слалома гиганта (ГС) не такая уж и большая - мене 20м/с для ГС - и повторяется от старта к старту с достаточно большой точностью. Такую же картину мы наблюдаем при анализе результатов другого лидера КМ - Теда Лигети.
К сожалению, ФИС не публикует официальные данные по протяженности конкретных спортивных трасс, а также данные по постановке ворот на этих трассах. Поэтому мы можем только оценить среднюю скорость спортсменов с точностью +/- 10%. Но для целей этой статьи этого будет вполне достаточно.
Главное, что скорость лыжника уровня КМ в трассе, как оказывается, не такая уж и большая и, фактически, она не сильно отличается от скорости катания продвинутого лыжника. И второе, лыжники уровня КМ демонстрируют примерно одинаковые скорости на совершенно разных трассах. Общее у этих трасс одно - примерно одинаковые средние расстояния между воротами при постановке трассы - около 12м для слалома, около 27м для ГС. При этом скорость лыжников уровня КМ в трассе слалома всегда несколько меньше, чем в трассе ГС.
В чем же секрет такой "медлительности" спортсменов? Оказывается, во всем виноват "эффект абсолютно упругого склона" именно он заставляет спортсменов ограничивать скорость при прохождении трассы.
"Эффект абсолютно упругого склона" заключается в следующем - чем ближе спортсмен приближает свой центр масс к поверхности склона, тем сильнее склон "отталкивает" ЦМ спортсмена, что приводит к отрыву от склона и фазе полета при достаточно больших скоростях движения спортсмена в резаном повороте. Как это происходит с Тедом Лигети на трассе слалома гиганта
отлично видно, что спортсмен пролетает по воздуху 6-7 метров.
Далее будет показано, что разгрузка лыж и фаза полета с последующей загрузкой лыж при достаточно большой скорости движения лыжника происходят помимо его воли, и что слаломиста склон "отталкивает" сильнее, чем гигантиста.
Максимально возможная скорость прохождения трассы определяется длительностью (длиной) фазы полета, которая должна соответствовать возможностям спортсмена приземлится на лыжи. С учетом существования достаточно интенсивного вращения тела спортсмена вокруг его центра масс в момент отрыва лыж от склона фаза полета не может быть слишком длительной.
Поэтому, спортсмен вынужден ограничивать свою скорость в трассе, несмотря на то, что каждый спортсмен хочет ехать «быстрее» и «ускоряться в каждом повороте».
Слаломисту приходится довольствоваться более медленной скоростью, так как дальность полета слаломиста больше чем у гигантиста при одинаковой скорости движения.
Этот "эффект абсолютно упругого склона" для резаного поворота (мы будем говорить только об этой технике) следует из самых общих соображений - принципа сохранения давления на склон, который я уже излагал в статье "Что должен делать лыжник, чтобы его лыжи надежно резали склон." и того факта, что величина силы нормального давления, которое лыжник оказывает на склон за время движения от вешки до вешки, неотрицательна и пропорциональна квадрату скорости движения лыжника. Время, которое лыжник затрачивает на прохождение расстояния от вешки до вешки обратно пропорционально скорости движения лыжника.
Если предположить, что лыжник не теряет контакта со склоном за время движения от вешки до вешки, то получим, что величина средней силы нормального давления за указанное время движения пропорционально величине скорости движения и возрастает неограниченно с ростом скорости. А это противоречит принципу сохранения давления на склон, согласно которому величина средней силы нормального давления при движении от вешки до вешки должна в точности равняться весу лыжника в покое. Поэтому лыжник, начиная с некоторой скорости движения часть времени движения проводит в воздухе. И чем больше скорость, тем большую часть времени движения от вешки до вешки лыжник должен проводить в полете.
Однако, как только лыжник потеряет контакт со склоном - окажется в состоянии невесомости - все будет определяться формулами о движении тела брошенного под углом к горизонту, которые всем известны с 8 класса средней школы.
Увеличивающееся с ростом скорости движения расстояние, которое вынужден будет пролетать лыжник после отрыва от склона, должно соответствовать параметрам трассы. Иначе лыжник просто "не впишется" в трассу.
Можно подумать, что максимальная скорость лыжника в трассе определяется самой трассой, точнее ее постановкой. Однако, это не совсем так. Конфигурация трассы должна соответствовать возможностям лыжника устойчиво пройти фазу полета - фаза полета не должна быть слишком длинной, так как тело лыжника в фазе полета сохраняет существенное вращение в плоскости перпендикулярной к направлению движения лыж в момент потери лыжами контакта со склоном. Если фаза полета будет слишком длинной, то лыжник просто не сможет "приземлиться" на лыжи.
Максимально возможная скорость прохождения трассы не изменится, если исчезнет сила трения лыж о снег и сопротивление воздуха - ее величина не зависит от этих факторов. При этом, если лыжник превысит эту максимальную скорость, то трассу он просто не пройдет. Поэтому задача у лыжника, проходящего конкретную трассу слалома (ГС и т.п.) одна – не превысить эту заданную трассой максимальную скорость, или – «хочешь ехать быстрее – тормози!».
Интересно, что для одной и той же трассы, поставленной на двух склонах разной крутизны максимальная скорость прохождения трассы на более крутом склоне будет МЕНЬШЕ максимальной скорости прохождения трассы на более пологом склоне.
Все вышесказанное следует из динамики резаного поворота. К сожалению, чтобы все пояснить, без формул уже не обойтись. Поэтому, те, кто не испытывает отвращения к физическим формулам и не забыл институтскую физику, читайте, пожалуйста весь текст статьи. Все выводы, сделанные в статье имеют строгое физическое обоснование.
Те, кто по каким-то причинам не любит физику могут сразу изучить выводы которые следуют из теоретической части статьи.
ВЫВОДЫ
- Для резаного поворота справедив "эффект абсолютно упругого склона" , то есть - на каких бы лыжах лыжник не совершал резаный поворот, начиная с определенной скорости движения его будет отрывать от склона. Причем, для достаточно больших скоростей движения лыжника, угол закантовки, при котором происходит отрыв лыж от склона, НЕ зависит от скорости движения лыжника и радиуса лыж, на которых едет лыжник, а зависит только от закантовки лыж в апексе резаного поворота. Или - угол отрыва есть универсальная функция от угла закантовки лыж в апексе.
- Для резаного поворота справедив второй вариант формулировки "эффекта абсолютно упругого склона" - начиная с определнной скорости движения лыжник сможет проехать по резаной дуге после апекса поворота только некоторое фиксированное расстояние, затем его лыжи оторвутся от склона. Причем длина этой резаной дуги НЕ зависит от скорости движения лыжника, но зависит от радиуса лыж (прямо пропорциональна корню квадратному из радиуса лыж), на которых едет лыжник, и зависит от закантовки лыж в апексе резаного поворота.
- Нормальная к поверхности склона составляющая скорости ЦМ лыжника в момент отрыва его лыж от склона пропорциональна скорости движения лыж в дуге поворота. Для достаточно больших скоростей движения коэффициент пропорциональности зависит только от угла закантовки лыж в апексе поворота. Поэтому, продолжительность безопорной фазы поворота - "полета" - прямо пропорциональна квадрату скорости движения лыж в дуге поворота. Из чего следует, что при увеличении скорости лыжник пролетает все большее расстояние, и при очень большой скорости это расстояние также будет очень большим.
- Длина фазы полета (дальность) пропорциональна квадрату скорости движения лыжника. Фаза ведения определяет почти все в повороте. Фаза полета не определяет почти ничего, кроме максимальной скорости движения лыжника. Фаза полета не должна быть слишком длинной, так как тело лыжника в фазе полета сохраняет существенное вращение в плоскости перпендикулярной к направлению движения лыж в момент потери лыжами контакта со склоном. Если фаза полета будет слишком длинной, то лыжник просто не сможет "приземлиться" на лыжи.
- Угол на который повернет лыжа при движении по дуге резаного поворота не зависит от скорости движения лыжника при достаточно больших скоростях движения. Величина угла поворота лыжи обратно пропорциональна корню квадратному из радиуса лыжи. При этом коэффициент пропорциональности зависит только от угла закантовки лыжи в апексе поворота (или от угла между голенью и поверхностью склона в апексе поворота). Для слаломной лыжи при угле закантовки в апексе поворота 700 угол поворота лыжи при движении по резаной дуге составляет около 800, при угле закантовки 800 угол поворота составляет 1400.
- Угол поворота ЦМ лыжника во время движения по резаной дуге в повороте также не зависит от скорости движения лыжника и для слаломиста примерно на 200 меньше чем угол поворота лыж, а для ГС лыж угол поворота ЦМ лыжника в резаном повороте - примерно на 100 меньше чем угол поворота лыж.
- Резаный поворот при спортивных скоростях состоит из двух фаз – фазы ведения лыж (резания) и фазы полета. Длина резаной дуги при больших скоростях движения лыжника не зависит от скорости движения лыжника и пропорциональна корню квадратному от величины радиуса лыж для одной и той же степени закантовки лыж в апексе поворота. Длина фазы полета (дальность) пропорциональна квадрату скорости движения лыжника. Фаза ведения определяет почти все в повороте. Фаза полета не определяет почти ничего, кроме максимальной скорости движения лыжника. Фаза полета не должна быть слишком длинной, так как тело лыжника в фазе полета сохраняет существенное вращение в плоскости перпендикулярной к направлению движения лыж в момент потери лыжами контакта со склоном. Если фаза полета будет слишком длинной, то лыжник просто не сможет "приземлиться" на лыжи.
- топовый спортсмен - слаломист как и гигантист проводит в полете примерно 30% времени при движении от вешки до вешки и угле закантовки лыж в апексе поворота в 70 градусов, лыжи спортсмена отрываются от склона при угле закантовки в 20-25 градусов. Так как уравнения механики могут быть инвертированы по времени, то, соответственно, спортсмен начинает загружать и закантовывать лыжи примерно с такого же начального угла закантовки.
- Спортивный резаный поворот осуществляется на сравнительно небольших скоростях, определяемых расстоянием между вешками трассы. Чем круче склон, тем меньше максимальная скорость прохождения трассы, так как проекция ускорения свободного падения на нормаль к склону уменьшается с увеличением крутизны склона, следовательно, расстояние, которое пролетает лыжник при одной и той же скорости его ЦМ при отрыве от склона будет увеличиваться. Поэтому максимально возможная скорость прохождения трассы на крутом склоне будет меньше, чем на пологом склоне (для одинаковых конфигураций трассы, разумеется)
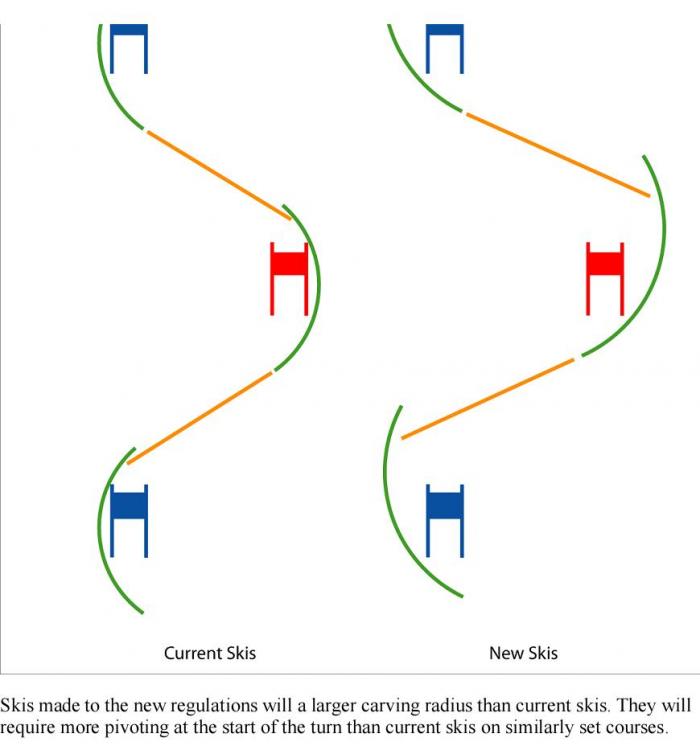
- Техники слалома и гигантского слалома кардинально отличаются друг от друга. В слаломе поворот (изменение направления движения центра масс лыжника в плоскости склона) происходит в основном за счет резаного ведения лыж и в небольшой степени за счет pivoting в начале фазы ведения. В гигантском слаломе pivoting дает примерно такой же вклад в поворот, как и резаное ведение. Поворот происходит за счет pivoting при приземлении лыж в начале фазы ведения и далее за счет резаного ведения. Причем резаное ведение в ГС повороте служит также для создания условий обеспечивающих исполнение pivoting в следующем повороте - обеспечения фазы полета. Это особенно выражено на крутых и жестких склонах.
- из расчетов статьи следует, что при увеличении радиуса лыжи роль и количество pivoning возрастает. На это указывал Ронлемастер http://www.ronlemaster.com/
Изложение для читателей, не забывших физику
Постановка задачи и некоторые определения.
Рассмотрим движение лыжника в дуге резаного поворота принимая за начальное положение лыжника его положение в апексе поворота. Без ущерба для общности рассмотрения будем считать, что лыжник едет с постоянной скоростью и на одной лыже.
Резаным поворотом назовем такой поворот при котором центр лыжи в каждый момент времени движется по дуге, радиус кривизны которой R в точке нахождения центра лыжи связан с углом закантовки А лыжи в этот момент известным соотношением R=R0cos(А).
Апексом резаного поворота назовем точку на дуге, вырезаемой лыжей, при прохождении которой центром лыжи, угол закантовки лыжи максимален (угол закантовки находится в локальном максимуме).
Пусть силы сопротивления отсутствуют. Будем считать, что трасса поставлена таким образом, что лыжник должен повернуть на максимально возможный для него угол, для чего лыжник должен достигать в апексе поворота максимальных углов закантовки и все время "упираться в лыжу", сохраняя неизменным расстояние между лыжей и своим центром масс во время поворота.
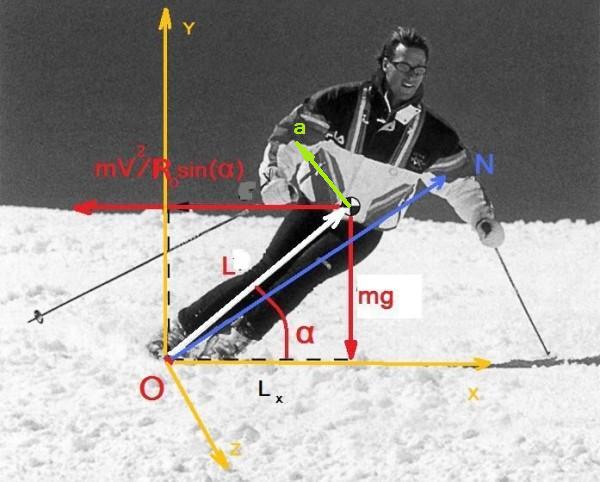
Движение лыжника будем рассматривать в «субъективной» для лыжника системе отсчета, в которой режущий кант лыжи покоится. Начало отсчета O совпадает с центром режущего канта лыжи (центром лыжи).
Ось Z этой системы отсчета совпадает по направлению с режущим кантом лыжи и направлена по ходу движения центра лыжи, ось Y направлена вверх и вдоль нормали к поверхности склона, ось X перпендикулярна осям Z и Y и лежит в плоскости склона и в любой момент времени перпендикулярна режущему канту лыжи.
Склон будем считать плоским. Угол наклона склона к горизонту - β.
Движения лыжника для наблюдателя, покоящегося относительно выбранной нами системы отсчета, выглядят примерно так, как изображено на фотографии (Рис.1).
(рис.1)
Будем считать, что лыжник, благодаря конструкции лыж, креплений и ботинок, удерживает свое тело (свой центр масс) в плоскости перпендикулярной лыжам и проходящей через центр режущего канта (цетр лыжи), то есть ЦМ лыжника движется все время в плоскости ХОУ. Все это можно принять без потери для общности рассмотрения.
Так как мы предположили, что лыжник во время движения поддерживает расстояние между своим ЦМ и режущим кантом постоянным, то ЦМ лыжника движется по дуге окружности постоянного радиуса L с центром в точке О, расположенной в плоскости XOY. Скорость движения ЦМ в общем случае не постоянна. Условие постоянства радиуса окружности по которой движется ЦМ лыжника позволяет в любой момент времени однозначно связать угловое ускорение ЦМ лыжника относительно оси Z с составляющей ускорения ЦМ лыжника, перпендикулярной радиус- вектору L, которая на схеме обозначена как а.
Пусть лыжник все время движется при отсутствии ангуляции, то есть угол закантовки его лыж А равен углу инклинации ЦМ лыжника внутрь поворота, то есть углу между осью Z и радиус-вектором ЦМ лыжника L. Строго говоря, резаный поворот при отсутствии ангуляции невозможно реализовать даже теоретически. Дело в том, лыжник действует на склон с силой равной по величине и противоположной по направлению силе реакции опоры N (синий вектор на рис 2.). При условии отсутствия ангуляции сила реакции опоры N для случая резаного поворота будет направлена как указано на рис 2. При таком направлении воздействия на склон лыжа будет все время выскальзывать из канавки, которую сама же нарезает и резаный поворот осуществить не удастся. Я не будувэтой статье объяснятьпричины по которым реакция опоры в случае отсутствия ангуляции будет направлена именно так, как показано на рис. 2, так как для целе данной статьи это не важно. Также,для того, чтобы не загромождать дальнейшие расчеты я буду считать, что угол ангуляции равен нулю, но лыжник все-таки едет резаным поворотом. Это никак не скажется на выводах данной статьи, так как то обстоятельство, что я пренебрег необходимым небольшим углом ангуляции практически не скажется на общей динамике поворота.
Пуcть в начальный момент лыжник находится в апексе поворота – угол закантовки А лыжи максимален, а острый угол α = π/2-А между голенью лыжника и поверхностью (плоскостью ХОZ) минимален.
(рис.2)
Выбранная система координат является неинерциальной. Так, начало отсчета этой системы, точка О, в каждый момент времени движется с постоянной линейной скоростью V по оружности радиуса R=R0sin(α), величина которого в общем изменяется во времени. Центр этой окружности все время перемещается в плоскости склона. В частности, для выбранной системы отсчета этот цент все время находится на оси Х. Сама система отсчета вращается вокруг оси У с угловой скоростью ω=V/R0sin(α), в общем также переменной во времени.
В выбранной системе отсчета на лыжника действуют три силы - сила тяжести - mg, сила реакции склона - N, примерное направление которой для больших скоростей движения лыжника указано на рис. 2 и сила инерции. Рассмотрим силу инерции подробнее.
В данном конкретном случае сила инерции, действующая на лыжника определяется тремя обстоятельствами:
1) ускоренным движением точки О относительно инерциальной системы отсчета, в которой склон покоится, что дает составляющую силы инерции величиной mV2/R0sin(α) направленную противоположно оси Х ,
2) вращением выбранной системы отсчета вокруг оси У с угловой скоростью ω=V/R0sin(α),
3) переменностью этой угловой скорости вращения во времени,
что дает вторую и третью составляющие силы инерции. Вторую - величиной mω2Lx , где Lx - координата Х ЦМ лыжника, направленную вдоль оси Х , а также силу Кориолиса - третью составляющую силы инерции величиной 2m[v,ω], где v - скорость движения ЦМ лыжника в плоскости XОY и силу эйлера - четвертую составляющую силы инерции величиной m[L,dω/dt], где L - радиус вектор ЦМ. [*,*] - векторное произведение.
Две последних составляющие силы инерции действуют в направлении, перпендикулярном к плоскости ХОУ, в которой происходит движение ЦМ лыжника и на это движение влияния не оказывают. Однако, эти силы, особенно сила Эйлера, могут иметь при больших углах закантовки лыж и больших скоростях движения лыжника достаточно большие величины, Эти силы ответственны за "отсаживание" лыжника в резаном повороте. Рассмотрению этого вопроса будет посвящена отдельная статья.
Будем считать, что радиус дуги оружности по которой в данный момент движется центр лыжи R много больше, чем Lx. При больших углах закантовки лыж это может дать погрешность 10-15%, но учет Lx слишком загромоздит расчеты, но не окажет заметного влияния на результат.
Зависимость величины острого угла α между голенью лыжника и осью Х от времени описывается простым уравнением моментов относительно оси Z, или относительно режущего канта лыжи ( рис.2).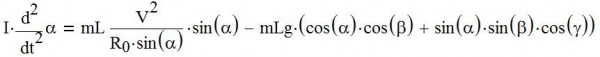
(1)
где Rо - радиус лыжи, I - момент инерции лыжника относительно оси Z, m - масса лыжника, L - расстояние от центра масс (ЦМ) лыжника до оси О, которое мы будем считать неизменным. В начальный момент (апекс поворота) α=α0 , dα/dt=0.
Угол наклона склона к горизонту - β = const. Угол γ(t) - угол между осью Х и тангенциальной к склону составляющей g (или направлением ЛПС)
Зависимость текущего радиуса поворота лыжи от угла α определяется хорошо всем известным соотношением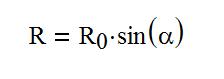 
из которого, учитывая, что γ(t) связан с R(t) известным соотношением можно вычислить кривую по которой в плоскости склона движется центр лыжи. Таким образом задача математически замкнута.
Некоторые замечания.
Уравнение (1) представляет из себя так называемую динамическую систему. В зависимости от параметров V - скорости движения лыжника, R0 - радиуса лыжи, L - расстояния от ЦМ лыжника до оси Z, уравнение (1) может иметь как стационарные решения ( решения которые не зависят от времени, а именно α=const) так и решения, зависящие от времени.
Стационарные решения уравнение (1) имеет в том случае, если при некотором α правая часть уравнения (1) равна 0. Таких решений - значений α=const - может быть несколько.
Стационарные решения (α=const) называют равновесной дугой или равновесным поворотом. Слово "равновесие" выражает тот факт, что угол между голенью лыжника и поверхностью склона остается постоянным в течение всего поворота. Такие решения могут быть как устойчивыми, так и неустойчивыми.
Однако, стационарные решения уравнения (1) при условии dV/dt >=0, существуют только для случая склона - горизонтальной поверхности β=0. Очевидным устойчивым стационарным решением уравнения (1) в этом случае является решение α=π/2 - .вертикальное положение тела лыжника. При небольших скоростях движения могут существовать и другие стационарные решения, как устойчивые так и неустойчивые.
Для склона при β>0 стационарных решений не существует, за исключением случая,когда лыжник едет по некоторой прямой (γ=const), например, точно вниз по склону и поддерживает корпус в нормальном к склону положении.
Особый интерес представляет случай, когда правая часть уравнения (1) является положительной величиной для любых допустимых значениях α β γ и для любого момента времени. В этом случае если в какой либо точке нормальная к склону составляющая скорости центра масс лыжника равна нулю, как в апексе поворота, например, то центр масс лыжника начнет ускоренное движение (вектор а на рис. 2) в сторону ОТ поверхности склона - угол α между голенью лыжника и поверхностью склона будет увеличиваться. Лыжник сможет завершить текущий поворот.
Если правая часть уравнения (1) является отрицательной величиной для любых допустимых значениях α β γ и для любого момента времени, то лыжник, в расммотренном выше случае просто упадет на склон.
Легко видеть, что правая часть уравнения (1) является ЗАВЕДОМО положительной величиной для любых допустимых значениях α β γ в случае, если V2/R0>g. В частности, это условие выполняется для достаточно больших скоростей движения лыжника.
Решение для очень больших скоростей движения лыжника.
Нас интересует ответ на вопрос статьи. Поэтому будем рассматривать движение лыжника с очень большими скоростями V. Тогда уравнение (1) можно преобразовать в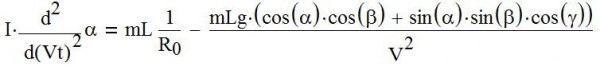
(2)
Очевидно, что при очень больших скоростях движения V вторым слагаемым в правой части уравнения (2) можно пренебречь.
В итоге получим уравнение, из которого можно найти угол α для любого момента времени после прохождения лыжником апекса поворота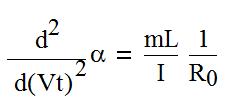
(3)
Мы получили очень интересный результат - положение ЦМ, определяемое в каждый момент времени углом α, остается неизменным в каждой точке дуги поворота для любой достаточно большой скорости движения лыжника.
Действительно, из уравнения (3) следует, что α является функцией только от произведения скорости движения на время - Vt. Или α = α(Vt)
Так как Vt - это расстояние, которое проходит лыжник вдоль дуги поворота за время t, то каждой точке на дуге поворота соответствует свой угол α, и этот угол не меняется при увеличении скорости движения лыжника.
Попробую пояснить этот факт - например, если заснять прохождение нашим лыжником поворота с двумя разными скоростями, то, замедлив фильм с более быстрым прохождением поворота, можно получить полное наложение изображения лыжника за все прохождение поворота для двух фильмов.
Можно сделать вывод, что если бы лыжник был "привязан к склону", то есть сохранял каким-то образом контакт со склоном в любой момент, то он бы ехал по одной и той же траектории независимо от скорости своего движения и мог бы пройти данную трассу с любой скоростью. Например, бусина, нанизанная на проволоку, будет двигаться по проволоке с любой наперед заданной скорость, повторяя все изгибы проволоки.
Отмечу, что решение вышеприведенного уравнения (3) дает для α формулу известную всем еще со школы, когда в 8 классе на уроках физики все проходили равноускоренное движение.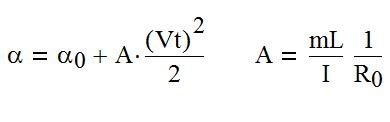
(4)
где α0 - угол наклона голени лыжника к поверхности склона в апексе поворота.
Момент инерции лыжника относительно оси О, с учетом того, что масса нижней половины тела человека составляет 40% от общей массы тела, с достаточно хорошим приближением равен
(4.1)
где L - половина роста человека при этом параметр А с учетом положения центра масс для этого случая определяется следующим образом
(4.2)
Хочу отметить, что численные результаты нашего рассмотрения пропорциональны квадратному корню из числового множителя в (4.2) и при достаточно заметном изменении момента инерции, влияние этого фактора на численные оценки не будет превышать 10%.
Но реальный лыжник к склону ничем не привязан и может потерять контакт со склоном при определенных условиях.
Условие (критерий) потери контакта со склоном простое - ЦМ лыжника должен в этот момент двигаться с ускорением в точности равным g - ускорением свободного падения.
Для нашего конкретного случая этот критерий выглядит следующим образом
(5)
где штрихами обозначено дифференцирование по времени. Левая часть соотношения (5) - это сумма проекций тангенциального и нормального ускорения ЦМ лыжника на ось Y. Левая часть соотношения (5) - это проекция ускорения свободного падения на ту же ось.
Воспользовавшись соотношением (4) после некоторых преобразований получим
(6)
Очевидно, что при больших V правой частью уравнения (6) можно принебречь.
Подставляя в уравнение (6) соотношение (4) для α после преобразований получаем
уравнение для определения αotr - угла между голенью лыжника и поверхностью склона при котором произойдет отрыв лыжи от склона при больших скоростях движения лыжника
(7)
где α0 - угол между голенью лыжника и поверхностью склона в апексе поворота
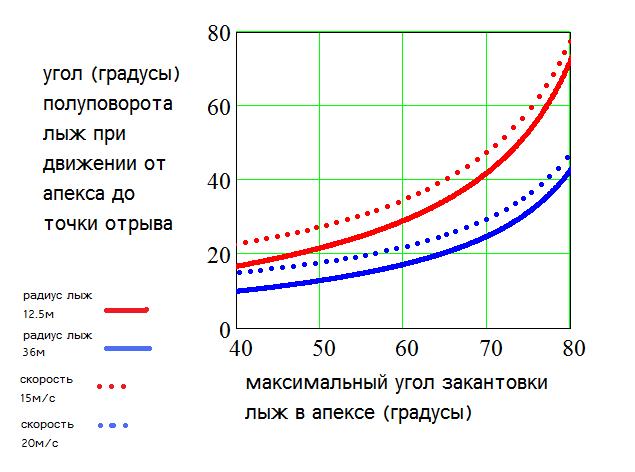
Мы получили еще один интересный результат - величина угла отрыва зависит только от начальной закантовки лыжи и не зависит ни от скорости движения лыжника ни от радиуса лыжи при больших скоростях движения. То есть αotrявляется функцией только от α0. Или αotr = αotr(α0) - универсальная функция для лыжника,совершающего резаный поворот.
Это и есть - "эффект абсолютно упругого склона" - на каких бы лыжах лыжник не совершал резаный поворот, начиная с определнной скорости его будет отрывать от склона. Причем угол закантовки при котором происходит отрыв лыж от склона НЕ зависит от скорости движения и радиуса лыж, на которых едет лыжник, а зависит только от закантовки лыж в апексе резаного поворота.
То есть лыжники на двух упомянутых наложенных друг на друга фильмах оторвуться от склона в одной и той же точке дуги. Или - длина дуги поворота, которую проходит лыжник от апекса поворота до точки отрыва от склона не зависит от скорости движения.
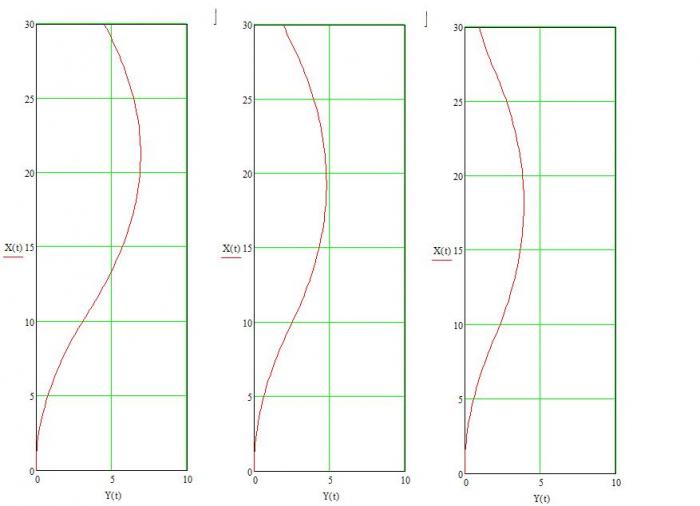
Приведу графическое решение соотношения (7) как зависимость угла, при котором происходит отрыв лыжника от склона αotr(α0) (углы измеряются в градусах - для удобства восприятия читателем)
(рис.3)
Для комплекса A(Vtotr)2 при помощи (4) получаем следующее выражение
(7.1)
где Ω(α0) выглядит следующим образом (α0 измеряется в градусах)
зная величину A(Vtotr)2 при заданном угле α0 получаем зависимость длины дуги ( Vtotr), которую проезжают лыжи от апекса резаного поворота до точки отрыва от радиуса лыжи для заданного значения α0.
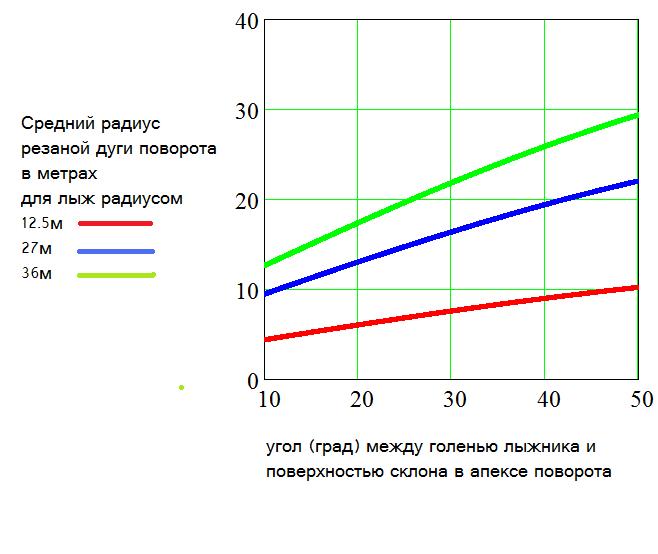
Это второй вариант формулировки "эффекта абсолютно упругого склона" - начиная с определнной скорости движения лыжник сможет проехать по резаной дуге после апекса поворота только некоторое фиксированное расстояние, затем его лыжи оторвутся от склона. Причем длина этой резаной дуги НЕ зависит от скорости движения лыжника, но зависит от радиуса лыж (прямо пропорциональна корню квадратному из радиуса лыж), на которых едет лыжник, и зависит от закантовки лыж в апексе резаного поворота.
Например, для α0=10, 20 и 30о, что является типичным значением для спортивного поворота, получим следующую зависимость для длины указанной дуги от радиуса лыжи (графики 1, 2 и 3 соответственно)
(рис.4)
Из этих графиков понятно, что решение ФИС увеличить радиус лыж для ГС до 36 м было разумным. Так же понятно как нужно ставить трассу для лыж соответствующего радиуса.
Время движения от апекса до точки отрыва totr для конкретной скорости движения определяется из приведенных графиков, учитывая, что длина дуги равна Vtotr или из соотношения (4),
Так как универсальная зависимость αotr от α0 нам известна, то с помощью соотношения (4) мы можем определить скорость ЦМ лыжника в момент отрыва и угол под которым эта скорость направлена к горизонту и далее по известным формулам можно определить время полета лыжника и расстояние, которое лыжник пролетит над склоном в фазе полета. При этом совершенно очевидно, что скорость отрыва ЦМ дыжника от склона пропорциональна текущей скорости движения и обратно пропорциональна корню квадратному из радиуса лыжи и также обратно пропорциональна корню квадратному от расстояния от оси О до ЦМ лыжника.
. Таким образом, лыжник после апекса поворота проедет некоторое ФИКСИРОВАННОЕ расстояние по склону и потом... отправится в полет.
Расстояние, которое проедет лыжник по склону в нашем случае от скорости движения не зависит (поэтому я назвал его ФИКСИРОВАННЫМ) и равно с хорошим приближением корню квадратному из радиуса выреза лыжи. Для слаломных лыж это расстояние - порядка 4 м.
Так как законы механики инвариантны относительно инверсии времени, то точно такое же расстояние лыжник проедет и до апекса поворота.
Угол Ψ, на который повернет лыжа за время резаного движения от апекса поворота до точки отрыва определяется следующим соотношением
(8)
и также не зависит от скорости движения (так как α является функцией от Vt, а totr обратно пропорционально V),
Чтобы это показать преобразуем (8), используя (4) и (7.1) - A(Vtotr)2 = Ω(α0) после соответствующей замены переменной в интеграле (8) получаем из (8) для Ψ следующее выражение
(9)
Очевидно, что угол на который повернет лыжа при движении по дуге от апекса поворота до момента отрыва от склона не зависит от скорости движения лыжника и обратно пропорциональна корню квадратному из радиуса лыжи. При этом коэффициент пропорциональности - интеграл в выражении (9) - зависит только от α0,
Величина этого коэфициента (в системе СИ) в зависимости от α0 - угла между голенью и поверхностью склона в апексе поворота (выраженному в градусах) выглядит следующим образом
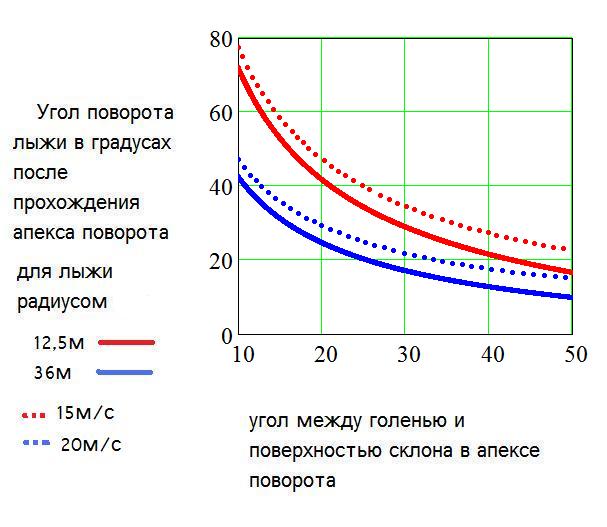
Приведу зависимость Ψ - угла на который повернет лыжа при движении по дуге от апекса поворота до момента отрыва от склона от α0 для лыж слаломной и ГС геометрии
(рис.5)
Интересно, что этот график доказывает безусловное преимущество резаного ведения лыж перед другими техниками поворота, так как при использовании резаного поворота слаломист, например, ТЕОРЕТИЧЕСКИ может повернуть на угол около 140о при ЛЮБОЙ скорости своего движения, что для других техник, связанных с проскальзыванием лыж, исключено.
Угол, на который повернет в плоскости склона вектор скорости ЦМ лыжника за время движения по резаной дуге будет несколько меньше, чем Ψ, но этот угол также не будет зависеть от скорости движения.
Покажем это. Используя соотношение (7.1) A(Vtotr)2 = Ω(α0) и соотношение (4) получим для скорости ЦМ лыжника относительно режущего канта лыжи в момент отрыва v
Тангенс угла между скоростью лыж и проекцией скорости ЦМ лыжника на склон определяется следующим образом
Приведу численные значения этого угла для разных α
Таким образом, угол поворота в плоскости склона вектора скорости ЦМ лыжника в резаном повороте также не зависит от скорости движения и для слаломиста примерно на 200 меньше чем угол поворота лыж.
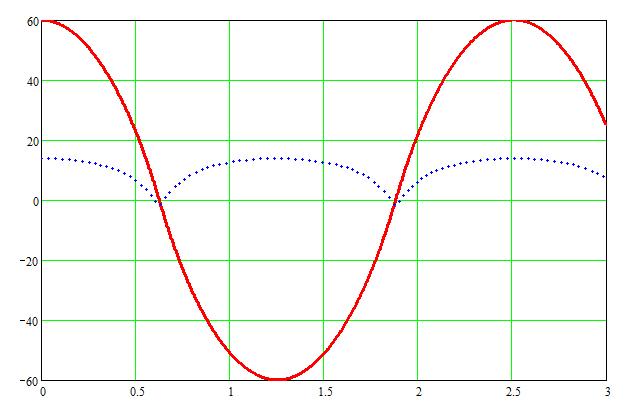
Сама же величина скорости отрыва пропорциональна скорости движения лыжника. Зависимость расстояния, которое пролетит лыжник при максимальном угле закантовки в апексе поворота 70о (α0=20о) от скорости движения лыжника для слаломных и ГС лыж приведено на этом графике
(рис.6)
Из этого рисунка становится очевидным ответ на вопрос "почему слаломист едет медленнее гигантиста" - при скорости, например, 20 м/с фаза полета слаломиста превысит 15 м - станет диннее, чем расстояние между вешками трассы (около 12м) и слаломист не сможет вписаться в трассу. Для гигантиста же, как видно, скорость 20 м/с является вполне "рабочей".
Чем быстрее движется лыжник, тем большее расстояние он пролетит по воздуху после отрыва от склона. Чтобы вписаться в 12 м трассу слаломист, например, не должен двигаться быстрее примерно 15 м/с. При бОльшей скорости лыжник просто не впишется в трассу, так как вне зависимости от скорости движения слаломисту на пути от одной вешки до другой вешки придется проскользить по двум разомкнутым дугам поворота 8-9 м (4-4.5м после первой вешки и 4-4.5м перед второй вешкой, что следует из рис.4) и пролететь некоторое расстояние между этими дугами по воздуху. Так как учетом кривизны дуг при 12 м трассе на полет останется 4-5м, то из рис.6 можно определить скорость движения лыжника, которая не должна превышать 15м/с.
Для трассы ГС, например, при 20м расстоянии между флагами, из рис.4 и 6 получаем - 14м скольжения плюс 7-8м полета. Из рис. 6 получаем для случая ГС примерно 20м/с.
А что же с горизонтальным разводом ворот? Влияет ли этот параметр на скорость прохождения трассы?
Из рисунка 5 следует, что если лыжник использует исключительно технику резаного поворота, то для слаломных лыж их поворот при резаном ведении доходит до 140о, что вполне соответствует разводу ворот на слаломных трассах, а вот для лыж ГС геометрии не превышает 80о, что мало для трасс ГС, которые мы наблюдаем на практике.
Объяснение этому обстоятельству простое - в обоих случаях спортсмен за счет приема pivoting заметно изменяет направление движения своего ЦМ в фазе приземления и врезает лыжи в начале поворота под некоторым углом к направлению скорости своего ЦМ, что обеспечивает бОльший итоговый угол поворота лыж.
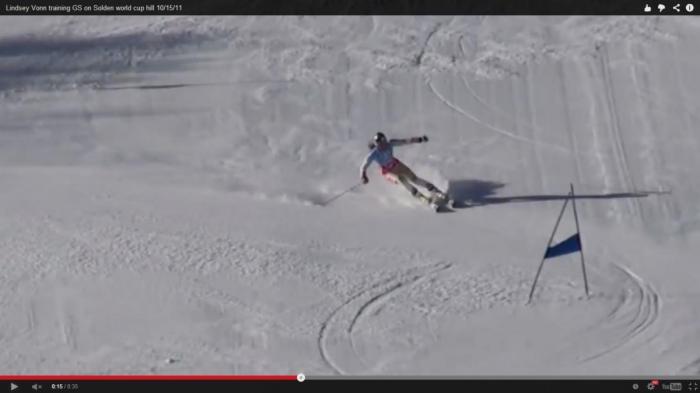
Причем в ГС поворот лыж происходит в основном с использованием этого приема - спортсмен врезает лыжи почти под прямым углом к направлению движения своего ЦМ в начале фазы полета при этом направление скорости ЦМ лыжника в этот момент не сильно отличается от направления лыж. Как это делает Вонн на трассе ГС. На фото начало и завершение pivoting. Лыжи спортсменки на последнем кадре еще не начали резать чистую дугу
Физической основой pivoting является анизотропия коэффициента трения скольжения о снег для лыжи, поставленной на кант и загруженной. Анизотропия - зависимость некоторой величины от направления в пространстве. Так лыжа поставленная на кант очень неохотно скользит поперек направления лыжи и оень охотно вдоль этого направления.
Рассмотрение физики этого явления выходит за рамки данной статьи. Однако прикидочный расчет показывает, что пивотинг позволяет повернуть вектор скорости ЦМ лыжника на угол сравнимый с аналогичным углом который дает резаная фаза ГС поворота и НЕ более того.
В слаломе pivoting применяется в гораздо меньшей степени, чем в ГС. Pivoting в исполнении Вонн при прохождении слаломной трассы можно увидеть на видео в конце статьи. Pivoting в исполнении Марселя Хиршера можно увидеть на этой раскадровке
Представляется, что бОльший горизонтальный развод ворот и пименение pivoting отчасти помогает спортсменам оганичивать свою скорость на крутых и жестких трасссах.
Мы видим, что расчитанные максимальные скорости прохождения трасс слалома и ГС не такие уж и большие, а я исходил из того предположения, что эти скорости ОЧЕНЬ большие.
Поэтому возникает вопрос применимости результатов этой статьи на практике.
Как это ни странно, все результаты остаются примерно такими же для скоростей движения лыжника 15-20м/с.
Так, например, рис. 3 при учете малости скоростей движения лыжника будет выглядеть так
(рис.7)
где красная линия - универсальная зависимость для больших скоростей движения, синие точки - зависимость для слаломных лыж и V = 15 м/с, зеленые точки - зависимость для ГС лыж (36м) и V = 20м/с.
Рисунок 4 для определения длины скольжения изменится следующим образом
(рис. 8)
где добавленные к рисунку 8 точечные графики имеют тот же смысл, что и для рис. 7.
Рисунок 5 изменится следующим образом
(рис. 9)
Рисунок 6 практически не меняется для небольших скоростей движения.
Уравнение (3) является хорошим приближением для описания движения ЦМ лыжника при небольших скоростях движения, правда для случая "классической ангуляции",
которую все применяют на практике. Это было показано мной в другой моей статье "Что должен делать лыжник, чтобы его лыжи надежно резали склон."
Поэтому все численные оценки, которые я привел выше, имеют к практике самое прямое отношение.
В частности, следующие оценки:
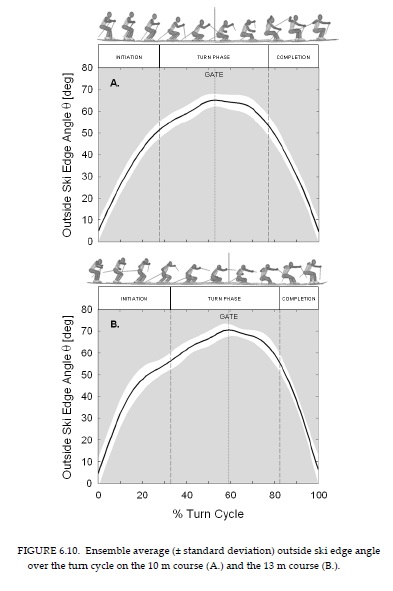
1) слаломист проводит в полете примерно 30% времени при движении от вешки до вешки,
2) его лыжи отрываются от склона при угле закантовки в 30-40о.
Как это хорошо видно на этом видео
чем для трассы слалома при одинаковом горизонтальном разводе ворот. Поправил текст.
55 поворотов на 1255 метров трассы получаем 22,8 метра между воротами если их поставить по прямой. Вот возьми за расстояние между воротами метров 27 и прикинь горизонтальный развод.
.
Ну, и принцип слегка противоположный. Обвесили датчиками несколько лыжников и описАли полученные измерения. 
- нам старперам, я подумал, так мерить сподручней будет.
Да и симпатичней Шифрин, на мой вкус
Тебе как? Вонн больше нравится, или Шифрин?
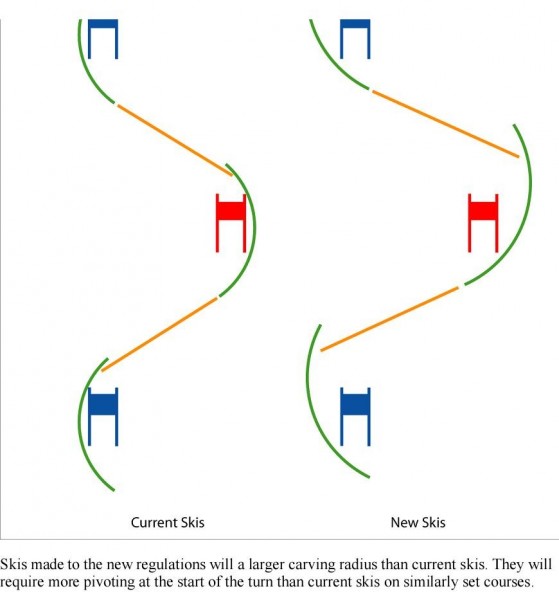
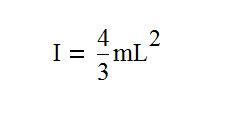
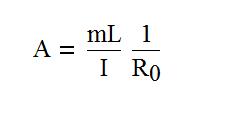
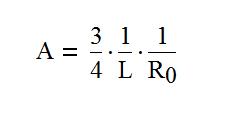
Никто не поставит одинаково трассу на склонах разной крутизны. Скорость действительно определяется постановкой, на крутых участках ставят более закрыто.