Математическая модель поворота с проскальзыванием на карвинговых лыжах
В опубликованных к настоящему времени работах, рассматривающих вопрос о математическом моделировании горнолыжного скользящего поворота, не учитывается параметры характерного для конструкции современных горных лыж бокового выреза определенного радиуса. Наличие такого выреза является одним из главных факторов поведения лыжи при выполнения любого поворота, включая поворот с боковым скольжением.
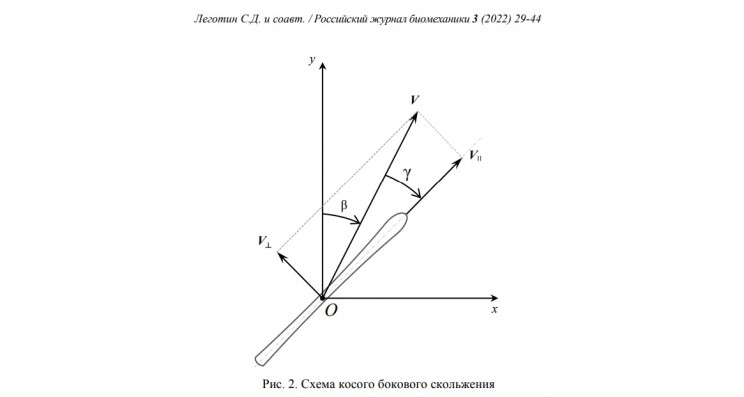
Представленная работа посвящена созданию численной модели движения механической системы "лыжник–лыжник" при выполнении поворота на карвинговых лыжах с боковым проскальзыванием и вибрацией. При этом рассматривается поворот в условиях относительного равновесия в системе отсчета, связанной с движущимся центром масс и с учетом управляемой лыжником ангуляции. В качестве основного допущения модели принимается предположение, что движение в скользящем повороте можно разложить на ортогональные направления: боковое скольжение и движение вдоль лыж по алгоритму, соответствующему чистому резаному повороту (карвингу) [18]. В модели производится учет сил сопротивления движению ‒ силы трения скольжения и силы аэродинамического сопротивления.
Для бóльшей общности и универсальности разработанная численная модель реализована для безразмерных параметров движения, а именно для описания безразмерных кинематических характеристик движения центра масс рассматриваемой механической системы. Получена система интегральных уравнений, с помощью которой можно найти скорость, время и траекторию движения центра масс, а также оценить углы, характеризующие положение тела лыжника и его лыж относительно склона при различных, задаваемых спортсменом стилевых ангуляциях. Созданная модель проиллюстрирована решением задачи для различных управляемых лыжником зависимостей угла скольженияю.
Вся работат находится тут.






















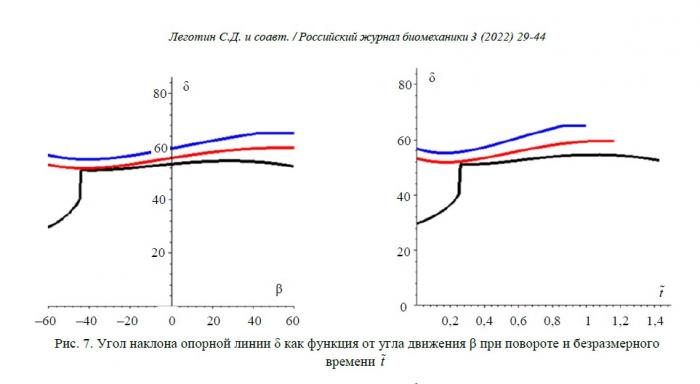

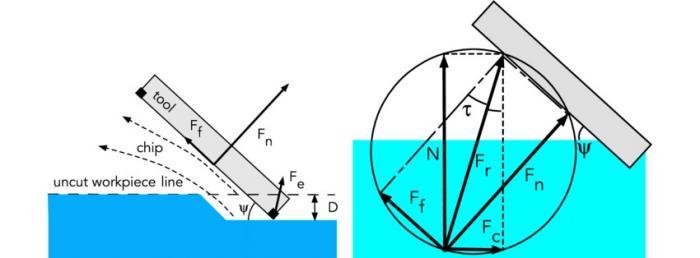

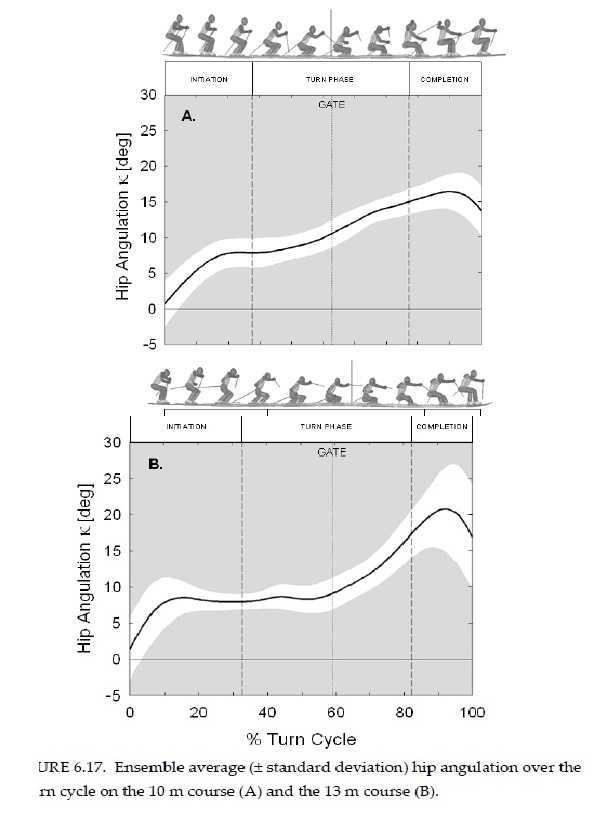

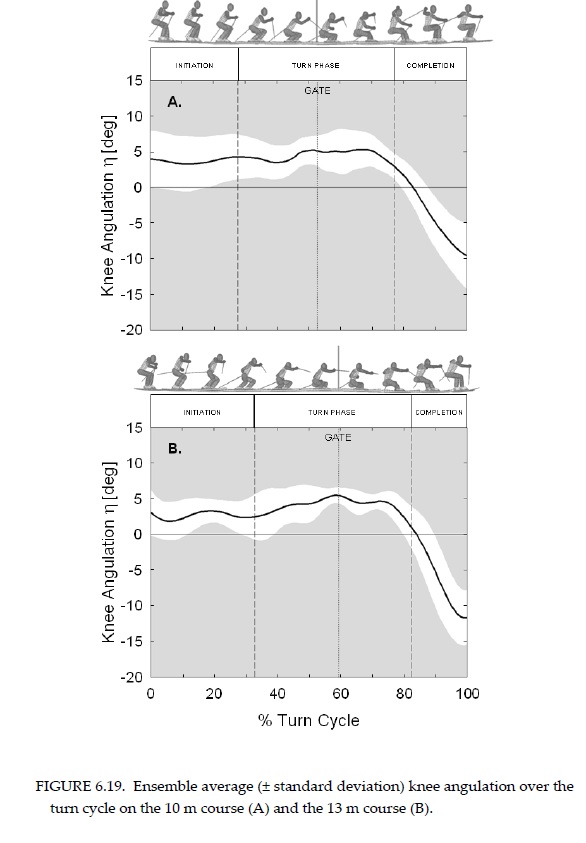




Вот, физики/математики! Ваш выход! То, что отдельная тема есть, и автор к тому же достойный спортсмен, отлично.