Конец сезона 07/08 ознаменовался появлением первой, в обозримой Skipper’ом истории, лыжи с изменяемой геометрией бокового выреза. Это Atomic Double Deck Vario Cut. Технология Double Deck была представлена в двух ипостасях: Vario Flex и Vario Cut. Если первая за истекший сезон 08/09 уже успела покрыть себя неувядаемой славой на спортивных трассах самого высокого уровня, то о второй мы читали пока только осторожные отзывы тестеров. Отзывы в целом положительные, но не отвечают на вопрос: а для чего нужна изменяемая геометрия и нужно ли она рядовому труженику снежных нив? Разве ему плохо и так, на новеньких карвовых, в богатом ассортименте, лыжах, сменивших собой совсем недавно, в историческом масштабе, приевшуюся «классику». Ещё не закончены споры между приверженцами карвинга и классического поворота, ещё кайтеры могут найти себе пару-другую завалявшейся в запасниках «классики». А тут, на тебе, лыжа с изменяемой геометрией! Между тем, для лыжестроения появление изменяемой геометрии лыжи сравнимо с появлением изменяемой геометрии крыла в авиации. Атомик, впрочем, проводит более скромные параллели: между «расщеплением» лыжи и расщеплением атома.
Поэтому есть резоны посмотреть, что же представляет из себя из себя новоявленная лыжа по сравнению с ... Но как же теперь называть «обыкновенную» карвинговую лыжу, которая - с неизменяемой геометрией? Если написать: «в отличие от традиционной лыжи...», то каждый будет понимать под традиционной лыжей именно классику. По небольшому размышлению я решил называть здесь «обыкновенную» карвинговую лыжу ординарной (велик могучим русских языка!), чтобы как-то вывернуться из этой ситуации.
Ниже мы попытаемся провести некоторый сравнительный анализ, но опираться нам придётся на что-нибудь более основательное, чем рекламные буклеты и отзывы тестеров. На имеющиеся, скажем, в наличии зачатки теории резаного поворота. Последние слова должны насторожить и послужить предупреждением читателям, испытывающим неодолимое отвращение ко всякого рода теориям. Хотя я и старался обойтись минимумом формул и графиков, но это мне не сильно удалось. Но тут уж ничего не поделаешь - иначе непонятно будет.
Но прежде чем что-то сравнивать, нам нужно уяснить, что же представляет в этом смысле и упомянутая нами «ординарная» лыжа. Что она позволяет делать и каким образом можно ей управлять. Поэтому мы с неё и начнем. Поскольку большая часть нижеследующего относится в равной мере как к лыжам, так и к сноуборду, мы будем далее пользоваться термином «лыжеборд», подразумевая под ним снаряд, на котором катается лыжебордер, - фигура, прочно вошедшая в лексический минимум читателей Скиру и иже с ним.
В одном серьёзном бордическом обзоре про карвинг, который вообще и в данном контексте следует понимать как катание сопряженными резаными поворотами, сказано много хороших и правильных слов и, в частности, приведено неплохое определение, которое, если перевести его, опять же, на великий и могучий, звучит примерно так: карвинг, в отличие от фрирайда и спортивных дисциплин, есть позволять лыжеборду ехать так, как ему хочется, следуя своей геометрии. Поэтому мы начнем с того, что попытаемся выяснить
1. Что хочет лыжеборд
 |
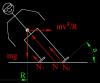
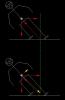
Из раскладки сил на приведенной картинке определяются условия бокового равновесия лыжника в повороте. Если к ним добавить ещё известную зависимость радиуса поворота ординарной лыжи от угла закантовки, которая собственно и определяет геометрию лыжеборда, то мы могли бы получить уравнения, связывающие параметры резаного поворота. Если бы это уже не сделали за нас. Подходящий нам вывод этих зависимостей можно найти в статье, подписанной ником Shyra на Onboard.ru. Подходящий, потому что рассматривается резаный поворот на горизонтальной поверхности, «незамутненный» нюансами, вносимыми крутизной склона и фазой поворота, отчего физика процесса остаётся достаточно простой. Там же приведены и расчетные характеристики для ряда радиусов бокового выреза досок. Всё это справедливо и для лыжника при преимущественной загрузке одной из лыж или, по крайней мере, при узком их ведении. Мы не будем повторять выкладки, но слегка модифицируем результаты, чтобы нам не возиться с различными радиусами.
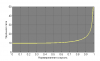
Из приведенных в указанной статье уравнений следует, что имеется некоторая предельная скорость Vпр, определяемая в более привычных нам обозначениях выражением
где Rо – радиус бокового выреза, при которой радиус поворота становится равным нулю. Мы, конечно, понимаем, что таких радиусов не бывает, поскольку лыжеборды по жизни так не гнутся. Это недостатки принятой модели, которая построена чисто из геометрических соображений и реальных характеристик лыжеборда не учитывает. Усложнять модель, чтобы уточнить этот параметр на несколько процентов, особого смысла нет. Следующий график даёт представление о числовых соотношениях между предельной скоростью и радиусом бокового выреза. Реально эта скорость несколько меньше.
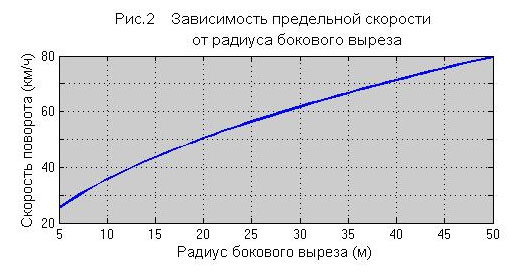 |
Если мы введем нормированную скорость vn = v/Vпр, где v – текущая скорость поворота, и нормированный радиус поворота rn = r/Ro , где r – текущий радиус поворота, то приведенные в статье зависимости параметров резаного поворота можно переписать в более простой нормированной форме:
 |
которая хороша уж тем, что позволяет обойтись единственной кривой для всех величин бокового выреза. Совместно с выражением для предельной скорости она полностью определяет характеристики лыжеборда для произвольной величины бокового выреза, что отражает, так сказать, единство геометрии. Соответствующие графические зависимости приведены на рис.3.
По нижней кривой видно, что наличие предельной скорости объясняется возрастанием до 90 градусов требуемого угла наклона. Физически это означает, что чистый резаный поворот со скоростью большей предельной для данной конкретной лыжи или борда невозможен. И вообще, резаный поворот – штука довольно капризная. Скорость, радиус и угол наклона жестко перевязаны между собой и не могут меняться произвольно. Поэтому достаточно рассматривать только кривую зависимости радиуса поворота от скорости. Это, можно сказать, базовая характеристика лыжи, поскольку плясать приходится именно от неё. Далее мы так и будем её называть
 |
На неё и наложены три подкрашенные и весьма нечетко определенные зоны, которые обычно не изображаются, поскольку малоинформативны в смысле резаного поворота по следующим причинам:
• зона слева соответствует малым скоростям, на которых кататься просто неинтересно: как видно, радиус резаного поворота в этой зоне практически не отличается от радиуса бокового выреза;
• зона снизу соответствует радиусам поворота, на которые реальный лыжеборд физически не может прогнуться;
• зона справа учитывает неточности используемой модели на скоростях, близких к предельной.
Далее мы не будем эти зоны обозначать явно, чтобы не затуманивать картинки, но будем иметь их в уме.
Как видно, собственно рабочий участок лыжи начинается где-то в районе 0,5Vпр, где радиус поворота начинает слегка отличаться от радиуса бокового выреза, и заканчивается при углах закантовки, которые может физически обеспечить лыжебордер, или при которых ещё в состоянии работать лыжеборд. Howe считает основной рабочей зоной лыжеборда, т.е. используемой по преимуществу большинством и в большинстве случаев, район 0,7Ro, что соответствует углам наклона/закантовки около 45 градусов.
У лыжебордера в рассмотренной «классической» постановке нет возможности произвольно менять радиус резаного поворота - только изменением скорости. «Для конкретной лыжи каждой скорости соответствует свой единственный радиус поворота» - пишет Howe. Это грустно. Но, как мы убедимся ниже, это не совсем так. И, пожалуй, самое неприятное в ординарном лыжеборде – это «противоестественный» характер зависимости радиуса поворота от скорости: на малых скоростях – большие радиусы, на больших – маленькие. Хотя логичнее было бы как раз наоборот.
Естественно, такое положение вещей не устраивает активного лыжебордера, и он начинает совершать различные телодвижения с тем, чтобы заставить снаряд ездить как-то поразнообразнее. И не без успеха. Так что нам имеет смысл посмотреть
2. Что может лыжеборд
Намек на возможность некоторого отхода от приведенных выше зависимостей сделан в уже упоминавшейся статье. Мы просто постараемся довести его до логического завершения.
 |
 |
Ну, а какую же «мощность ангуляции» может развить лыжебордер? Тёмное это дело, и зависит оно от снаряда, стойки и физических кондиций. Если лыжник «симметричен» в этом смысле и «ангулирует» посредством сложноскрученных изгибов в суставах, не всегда для этого предназначенных, то бордеру во фронтсайде ничего не стоит поставить борд как угодно за счет простого сгибания коленей. Но в другую сторону они гнутся плохо, поэтому возможности ангуляции в бэксайде у бордера куда как слабже. Поэтому не будем отвлекаться и сразу же забудем про то, кто чего и сколько может. Это их личное дело.
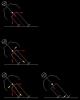
Посмотрим, как влияет ангуляция на равновесие лыжебордера в повороте. Ясно, что если лыжебордер не едет, а просто стоит на месте, то он может позволить себе ангуляцию хоть в 90 градусов, и от этого равным счетом ничего не произойдет. Другое дело – движение. Представим себе, что лыжебордер совершает на некоторой скорости некий «правильный» поворот без ангуляции, с некоторым углом наклона, который мы будем в данном случае именовать α0, чтобы подчеркнуть, что ангуляция нулевая. Затем он решает этот поворот «углубить» за счет ангуляции, для чего и принимает некоторое положение, обеспечивающее угол ангуляции β. В результате увеличивается угол закантовки лыжеборда и, соответственно, уменьшается радиус поворота. Это, в свою очередь, приводит к возрастанию центробежной силы и к нарушению условий равновесия. Поэтому лыжебордеру одновременно с ангуляцией необходимо озаботиться увеличением угла наклона на некоторую величину, которая компенсировала бы возрастание центробежной силы.
 |
Предположим, что он это сделал. Но увеличение угла наклона также приводит к увеличению закантовки и центробежной силы. Поэтому лыжебордеру следует озаботиться... и добавить ещё немножко угла наклона. Далее процесс, как вы понимаете, зацикливается. И, в зависимости от величины ангуляции, из него есть два выхода: либо он заканчивается некоторым конкретным значением Δα, которое следует добавить к α0, чтобы компенсировать ангуляцию, либо это добавление будет продолжаться до тех пор, пока угол закантовки не достигнет 90 градусов.
Естественно угол ангуляции, при котором этот процесс ещё является сходящимся, назвать предельным. Он может быть вычислен на основе только что приведенных рассуждений. Расчетные зависимости этого и прочих углов и их комбинаций от скорости поворота приведены рис.6. Предельный угол ангуляции на рисунке обозначен β*. Как видим, он решительно падает с ростом скорости и обращается в нуль при скорости равной предельной. Что тоже понятно, так как на этой скорости «ангулировать» уже некуда. Теперь угол закантовки, который раньше, в отсутствие ангуляции, определялся только синей линией, определяется линией зеленой, которая складывается из синей, желтой и красной. Зеленая линия определяет нам некоторый радиус резаного поворота, про который тоже просится сказать «предельный», но это не так. На графике рис.7 он представлен красной линией и обозначен r*. Синяя линия, обозначенная r0, есть радиус поворота в отсутствии ангуляции, то есть базовая характеристика лыжи. Тайный смысл красных линий на рис. 6 и 7 явится нам несколько позже.
 |
Ещё раз подчеркнем, что «красные линии» определяются механикой резаного поворота, а не способностью лыжебордера к ангуляции, поэтому - большой вопрос, способен ли лыжебордер использовать их в полной мере. Предположим, что способен. Что же произойдет, если он исполнит ангуляцию на угол, больший предельного для данной скорости? Да ничего особенного - его просто перекинет через лыжеборд на другую сторону. То же самое произойдет, если он выполнит ангуляцию, меньшую предельной, не увеличив при этом соответственно угол наклона. Это удобно, и лыжебордер часто этим пользуется в конце поворота.
Смысл дальнейшего проще всего пояснить, если рассмотреть графическое решение уравнения равновесия, которое приведено на рис. 8. Равновесие есть баланс весовой компоненты, представляющей собой момент силы веса относительно точки опоры и центробежной компоненты – момента центробежной силы.
 |
На рис. 8 желтая линия представляет график изменения весовой компоненты от угла наклона, а синие линии – графики изменения центробежной компоненты для некоторой конкретной скорости. Точки пересечения этих графиков соответствуют положениям равновесия лыжебордера в повороте. Желтая линия остаётся неизменной, а вот синяя меняется в зависимости от скорости и угла ангуляции. Пунктирная синяя линия соответствует случаю отсутствию ангуляции. Она имеет всего одну точку пересечения (1) с желтой, именно ту, для которой значение угла наклона соответствует графику на рис. 3.
При наличии ангуляции картина уже меняется – появляется вторая точка пересечения (2) и, соответственно, ещё одно положение равновесия. То есть при одной и той же скорости мы имеем два различных угла наклона, при которых обеспечивается равновесие лыжебордера в повороте. Это уже разнообразие. Но ещё не всё.
По мере увеличения ангуляции синяя кривая сдвигается влево ровно на такое же количество градусов, при этом, как видно из рис.8, точки 1 и 2 начнут сближаться, пока не сольются в одну, когда желтая и синяя кривые будут только касаться. Дальнейшее увеличение ангуляции приведет к тому, что точек пересечения уже не будет. И положения равновесия тоже. Это предельное значение ангуляции и соответствует тому, что изображено на рис. 6. красной линией.
Проделав такие построения для различных величин скорости мы можем построить более ли менее полную картину влияния ангуляции на параметры резаного поворота.
 |
Синие линии на графиках – это решения, соответствующие точке 1, а серые соответствуют точке 2, и, прежде чем что-либо сказать о полученных зависимостях, вернемся к рис.8 и посмотрим на точки 1 и 2. Характер пересечения синей и желтой линий у них разный. В точке 2 синяя линия после пересечения идёт выше желтой по мере увеличения угла наклона, а это означает что центробежная компонента больше по величине, чем компонента от силы веса. Но сила веса стремится «уронить» лыжебордера внутрь поворота, тогда как центробежная сила стремиться опрокинуть его наружу. Если мы предположим, что лыжебордер отклонился от положения равновесия, определяемого точкой 2, в сторону увеличения угла наклона, т.е. внутрь поворота, то баланс сил нарушается и преобладающая центробежная компонента вернет его обратно в положение равновесия. То же самое произойдет, если он отклонится от положения равновесия в другую сторону. В этом случае преобладающей будет уже весовая компонента, которая будет «ронять» лыжебордера, т.е. тянуть его снова в положение равновесия. В точке 1 всё как раз наоборот: при любом отклонении от положения равновесия соотношение действующих сил таково, что будет стремиться это отклонение увеличить. Соответственно, точка 1 является точкой неустойчивого равновесия, а точка 2 – точкой устойчивого равновесия. В этом, в общем-то, ничего особенного нет. При наличии нескольких положений равновесия устойчивым является самое нижнее. Гимнаст, выполняющий стойку на перекладине, находится в положении неустойчивого равновесия, которое он вынужден поддерживать, прилагая какие-то усилия по сохранению равновесия, а вот если он просто висит на перекладине, то находится в положении устойчивого равновесия, и для того, чтобы его сохранить, ему не нужно делать ровным счетом ничего. В этом и есть, небольшая, но в целом приятная разница между этими двумя типами равновесия.
Таким образом, на рис.9 красная линия, которую мы уже видели на рис. 7, для радиусов и жирная синяя линия для углов наклона разделяют области неустойчивого (синие линии) и устойчивого (серые линии) равновесия. Вертикальное сечение для какой либо скорости даёт в пересечениях с семействами этих линий достижимые параметры поворота для разных величин ангуляции. Но не будем забывать про «красные зоны», которые мы изобразили ещё на рис.3. Если мы наложим их на верхнюю картинку рис.9, то можно увидеть, что останется значительная часть области устойчивого равновесия, в которой параметры поворота вполне реальны. К тому же левая зона, которая определялась «малоизменяемостью» радиуса поворота, теперь может и вовсе не приниматься во внимание.
Что же в целом следует из предпринятого нами небольшого исследования? В общем-то, графики говорят сами за себя. Следует, что посредством ангуляции сухое меню радиусов поворотов, предлагаемое «хотящим» лыжебордом, можно существенно разнообразить, включая и такое экзотическое блюдо, как «зона устойчивого равновесия». Что это такое, и как оно проявляется в отношении лыжебордера, - с этим ещё предстоит разбираться. Ясно, что равновесие лыжебордера в повороте – достаточно сложная вещь. Поэтому не будем спешить с выводами. Но один очевидный вывод мы всё-таки сделаем: поворот одного и того же радиуса может быть выполнен на скорости тем большей, чем меньше величина ангуляции. Это, как не крути, опять же вода на мельницу ГГ.
Обратим внимание на то обстоятельство, что все наши «манипуляции с ангуляцией» никак не позволяют выскочить за пределы области, ограниченной базовой характеристикой лыжеборда.
Исчерпываются ли этим «карвинговые» возможности лыжеборда? Нет, конечно. Все приведённые зависимости получены из чистой геометрии и условий равновесия лыжебордера. И они эти условия обеспечивают. Т.е. лыжбордер, в отсутствие сопротивления, может крутиться в повороте, как яблочко по тарелочке, пока голова не закружится. Реальные повороты быстротечны, и лыжебордер может позволить себе кратковременную потерю равновесия в одном повороте, с тем, чтобы восстановить его в другом. Иными словами, чем длиннее дуга поворота, тем строже должны выдерживаться эти зависимости. Да и поведение лыжи на реальном снегу далеко не так «геометрично».
Тем не менее, теория даёт хорошее приближение к реалиям. Основоположники это проверяли. Но реалии шире. Равномерные загрузка и прогиб лыжеборда, подразумеваемые теорией, безусловно используются, но, помимо этого, на практике широко распространены «силовые» методы «руления» прогибом.
| «Carving is totally different from freeriding, because carvers strive to never skid the board. Carving is different from racing because the intent is to follow the decambered sidecut radius of the board, not the turn radius needed to pass a gate. As a result, carving has its own unique feeling of efficiency and perfection.» /Альманах карвера/ |
| «Зачем нужно загружать себя всей этой физикой? Вам, конечно, не требуется столько теории, потому что наше тело само чувствует равновесие. Но, возможно, понимание физики карвинга поможет вам рассмотреть те аспекты вашего катания, о которых вы не задумывались.» /Физика резанного поворота на сноуборде/ |
Другие статьи автора на сайте
Виртуальный бугор и разгрузка вниз
Две оси на одно колено
По следам «Пяти навыков…»
Закантовка. Технический роман из жизни лыжи в двух частях с иллюстрациями
Лыжные травмы коленей
Лыжи и светлое будущее
Ещё раз про внутреннюю лыжу
Карвинговая лыжа. В поисках идеала
Лыжи и оружие пролетариата
Занимательная геометрия для любознательного лыжника (в 2-х частях)
Atomic Double Deck и перманентная революция
| Автор: Игорь Изыльметьев |


















 Снова поменял лыжи и, несмотря на то, что цех ужел подтупился, все так же надежно держал.
Снова поменял лыжи и, несмотря на то, что цех ужел подтупился, все так же надежно держал. 




Ау!