Про карвинг, лыжеборд и Atomic Vario Cut

Начнем с небольшой цитаты:
«... – А что со сноубордом? – встрепенулся я в конце разговора.
– Да вот, за спиной стоит как раз сноубордический тренажер, – улыбается Мануилов. – Мало того, теория в случае сноуборда расписана более правильно, почти идеально – один-единственный кант, по которому и идет доска, – поэтому модель точнее.
– А что мешает разработать такую же стройную теорию для горных лыж?
– Не поверите – вторая нога у горнолыжника...».

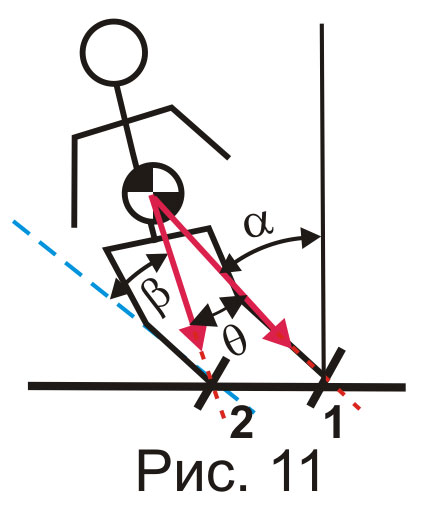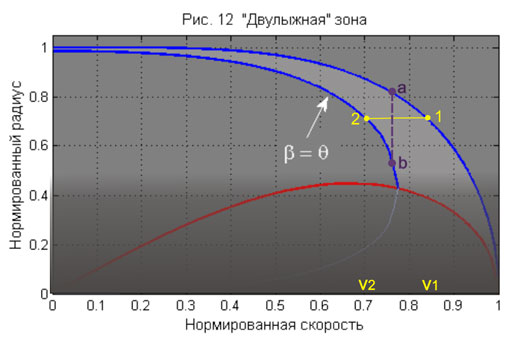
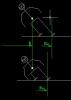
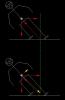
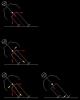
Предположим, что лыжник движется в повороте с некоторой скоростью V1, такой, что линия действия равнодействующей силы проходит точно через кант наружной лыжи. Т.е. лыжник движется, по сути, на одной лыже, и, как мы нарисовали, в отсутствие ангуляции. Это мы уже рассматривали, и поворот будет определяться базовой характеристикой лыжи для скорости V1. Далее мы предполагаем, что скорость лыжника постепенно падает, а лыжник не предпринимает никаких телодвижений, сохраняя абсолютное хладнокровие. Он имеет на это право, пока скорость не упадет до некоторого значения V2 < V1, при котором равнодействующая сила проходит через кант внутренней лыжи. Лыжник опять оказывается на одной лыже, теперь уже внутренней, но с величиной ангуляции β, которая, как легко углядеть из рисунка, при этом в точности равна θ. Этот случай мы тоже уже рассматривали. Поворот будет определяться точкой некоторой кривой, подобной изображенным на рис.9, соответствующей ангуляции θ и скорости V2.

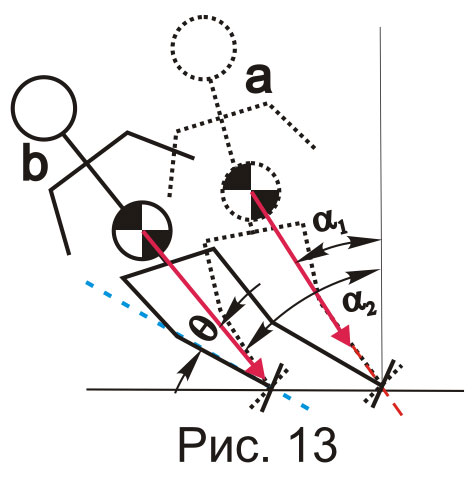
А что же происходит между этими двумя крайними положениями? По мере падения скорости от V1 до V2 угол наклона постепенно уменьшается на величину θ, и появляется некий угол ангуляции β, который при скорости V1 становится равным θ. Т.е. угол наклона плавно перетекает в ангуляцию. Но угол закантовки лыж каким был, таким и остался, - он при этом не меняется. Соответственно не меняется и радиус поворота.

Что же мы имеем в итоге? Да, лыжник располагает некоторыми преимуществами по части управления резаным поворотом за счет широкой постановки лыж и распределения нагрузки между ними. Но может ли он сделать что-нибудь такое, чего не может повторить бордер? Да нет, все его возможности в смысле резаного поворота лежат в той же внутренней области, ограниченной сверху базовой характеристикой, которая в равной мере справедлива и для борда. И за пределы этой базовой характеристики лыжник выскочить не может, несмотря на наличие двух лыж, двух ног и двух палок. И тут мы, наконец, подходим к основному вопросу, с которого мы начинали:

Мы разобрали достаточно подробно различные варианты управления резаным поворотом, и можем смело сказать, что у лыжебордера мало возможностей вырваться за пределы, очерченные базовой характеристикой лыжеборда. Точнее, только методы, описанные в разделе 3, могут как-то претендовать на отход от предписываемых базовой характеристикой закономерностей, но и они, в свою очередь, могут трактоваться как искусственное изменение радиуса бокового выреза, т. е. изменение, опять же, базовой характеристики лыжеборда, при этом малопонятным образом. Отсюда следует достаточно неоригинальный вывод: если мы хотим целенаправленно управлять резаным поворотом в больше мере, чем это позволяется ординарным лыжебордом, то нам следует управлять базовой характеристикой, или, что то же самое, радиусом бокового выреза, который её и определяет.

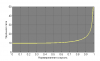
В этом и состоит, собственно, суть технологии, названой Атомиком «Vario Cut». Как устроены и работают эти лыжи, мы уже писали, поэтому не будем повторяться, и для дальнейшего используем только числовые данные, заявленные производителем. Всё, ранее сказанное про ординарный лыжеборд, относится, конечно, и к данной технологии, поэтому мы ограничимся рассмотрением только базовых характеристик. К сожалению, у нас нет реальных зависимостей радиуса бокового выреза этой лыжи от угла закантовки, но мы не сильно ошибёмся, если предположим, что радиус бокового выреза лыжи Atomic Vario Cut меняется линейно от максимального значения до минимального в диапазоне углов закантовки от 0° до, скажем, 70°. Мы можем несколько потерять в форме, но начальная и конечная точки кривой, так же как и общий её характер будут примерно те же. Тут нам для наглядности придётся отказаться от нормированной формы представления базовой характеристики, поскольку мы будем иметь дело с различными радиусами и, соответственно, с различными предельными скоростями. С учетом сделанных оговорок базовая характеристика лыжи «Vario Cut» будет иметь примерно такой вид, какой изображен на рис. 14.

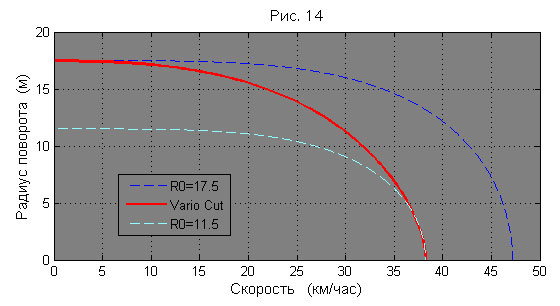Если сравнить характеристики лыжи «Vario Cut» и ординарной лыжи с радиусом бокового выреза 11,5 м (а сравнивать нужно именно их, поскольку этот радиус определяет предельную скорость для «Vario Cut»), то видно, что, по сравнению с ординарной лыжей, технология «Vario Cut» обеспечивает существенно больший диапазон радиусов поворота в том же диапазоне скоростей. Это безусловный плюс технологии, поскольку получается лыжа с более широкими возможностями резаного ведения поворота. Можно сказать, что эта технология как бы «растягивает» характеристику 11,5 метровой лыжи по оси радиусов до значения 17,5 метров.

В этом собственно и состоят теоретические предпосылки данной технологии. А во что они выливаются на практике, все, наверное, уже читали. Это в нашей простенькой теории для горизонтальной плоскости есть прямая связь между скоростью и углом закантовки, определяющим радиус бокового выреза. В реальных условиях на реальном склоне всё не так просто. И сам склон, и все вариации рельефа влияют на угол закантовки безотносительно к скорости и «нарушают», так сказать, «теоретическую чистоту». Это свойственно и ординарной лыже, но Vario Cut реагирует значительно сильнее в силу своей конструкции. Мы не будем утверждать, что это хорошо или плохо, - просто это другая лыжа, по-своему интересная.

Однако в рамках этой технологии можно сделать и лыжу, которая не подчеркивала бы склон и рельеф, а, наоборот, ослабляла. Ведь Атомик мог с таким же успехом поступить ровно наоборот: начинать с минимального радиуса бокового выреза при малых углах закантовки и заканчивать максимальным при больших. Ему для этого и особо делать-то ничего не нужно, – по другому пазы пропилить. Не знаю, рассматривали ли они этот вариант, но мы рассмотрим. Для этого случая базовая характеристика лыжи с «условным» названием «Vario Cut 2» будет выглядеть примерно так, как изображено на рис. 15.

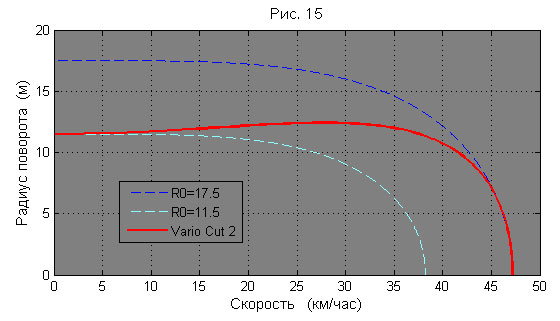Легко видеть, что по сравнению с ординарной лыжей в 17,5 м этот второй Vario Cut выглядит гораздо занимательней: характеристика начинается с малых радиусов и с небольшими отклонениями сохраняет их в большем диапазоне скоростей Можно примерно сказать, что мы растянули базовую характеристику, соответствующую минимальному радиусу, до скоростей, определяемых максимальным.

Всё это звучит довольно отвлеченно, поэтому попробуем перефразировать как-нибудь в околоспортивных аналогиях.

Если забыть про конкретные числовые значения, и положить, что минимальный радиус бокового выреза этих лыж соответствует слаломному, а максимальный – гигантскому, то можно сказать, что в первом варианте лыжи позволяют совершать на слаломных скоростях повороты с радиусами от слаломного до гигантского, а во втором – повороты со слаломными радиусами на скоростях от слаломных до гигантских. Можно сказать, что оба варианта выглядят привлекательно. И так хорошо, и так неплохо.

Поэтому мы могли бы спокойно на этом месте закончить с Vario Cut’ом, если бы не вопросы, которые возникают. Vario Cut – это, так сказать, первая веха на дороге, именуемой «изменяемая геометрия лыжи», и нас интересует, куда ведёт эта дорога, и ведёт ли она к храму? Всеобщего лыжного счастья.

И главный вопрос, который возникает: а как надо управлять геометрией лыжи? И тут мы должны развести руками, потому что ответа на него пока ни у кого нет. А раз его нет, то его следует придумать, и Атомик своё слово уже сказал. И, будем надеяться, не последнее. Мы тоже можем внести посильную лепту. Отталкиваясь от нашей аналогии, можем сказать, например: «А дайте нам лыжу, которая на слаломных скоростях поворачивала бы как слаломная, а на гигантских скоростях – как гигантская». Но не дадут. Пока, по крайней мере. Возможностей пока нет. Надеюсь, для читателей уже стало очевидно, что для эффективного управления базовой характеристикой лыжеборда следует управлять непосредственно по скорости движения лыжебордера в повороте, а не опосредованно, как это выполнено в Vario Cut . Так что для воплощения «нашей мечты» предстоит ещё изобрести методы и технические средства измерения скорости и непосредственного управления радиусом бокового выреза в зависимости от неё. Это вряд ли возможно без применения электронно-механических устройств, но это в «лыжном царстве» уже далеко не новость. Мы не будем вдаваться в технические и технологические сложности реализации всех этих устройств, зная уже по опыту, что ничего невозможного нет. А посмотрим, что мы можем с этого иметь.

Имея информацию по скорости мы сможем формировать любую характеристику в пределах, ограниченных диапазоном изменения радиуса бокового выреза. Правда, сначала нужно сообразить, а какую же характеристику нужно сделать. Но это уже вопрос вторичный, его отработают и откатают опытным путем. А для примера вспомним слова Howe о том, что наиболее используемый радиус поворота ординарной лыжи составляет 0,7R0, и нарисуем характеристику некоторой «перспективной» лыжи исходя из лозунга «пусть всегда будет 0,7!» Для этого достаточно обеспечить функциональную зависимость радиуса бокового выреза от текущей скорости R0 = 1,38V2/g , которую легко получить из выражения для предельной скорости. Как бы выглядела такая характеристика для данных Vario Cut - изображено на рис. 16.

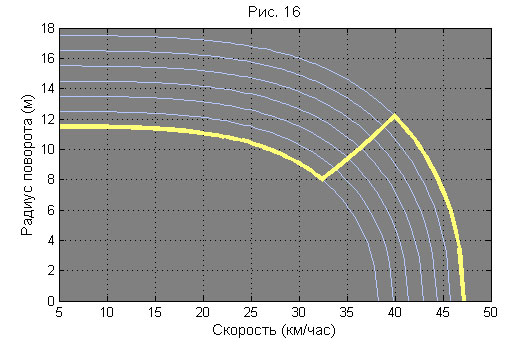В диапазоне скоростей на линейном участке радиус поворота будет в точности равняться 0,7 от текущего радиуса бокового выреза, а угол наклона будет постоянным и равным 45 градусам.

Таким образом, располагая информацией о скорости мы сможем формировать достаточно замысловатые базовые характеристики, но, так сказать, однозначные, где конкретной скорости соответствует определенный радиус поворота и определенный угол наклона. Если же научиться определять и угол наклона, что не бог весть какая задача, то можно заставить систему, управляющую радиусом бокового выреза, трактовать любое отклонение угла наклона от заданного базовой характеристикой как наше желание изменить радиус поворота на такой, при котором данный угол наклона соответствовал бы равновесному состоянию. То есть мы получаем возможность изменять радиус поворотов на одной и той же скорости. То есть теперь вместо желтой линии будет желтая полоса, покрывающая все характеристики от минимальной до максимальной. И это, заметьте, будут чистые резаные повороты, а не какое-нибудь «псевдо»! Лыжа будет автоматически подстраиваться под «клиента», обеспечивая его равновесие и, естественно, благополучие.

Далее уже пойдёт «тюнинг»: можно будет учесть и склон и фазу поворота, т.е. всё по-полной, а если занести, например, трассу SL, GS или DH во встроенный в лыжу GPS-навигатор, то он оптимизирует траекторию и будет извещать спортсмена об отклонениях от неё голосом ГГ.

Только вот, пожалуй, чего будет не хватать этой замечательной лыже для полной универсальности – так это длины. Всё-таки, для больших скоростей лыжа должна быть длиннее, чем для малых. Но и тут ничего невозможного нет, - на мой взгляд, конструктивно задача изменения бокового выреза хорошо сочетается с задачей изменения длины лыжи, так что, вполне возможно, мы скоро увидим и такое «комплексное» решение.

Вот такие нездоровые мысли вызывает появление изменяемой геометрии. Так что, придя в лыжный салон в недалеком будущем и увидев всё это великолепие, мы, вздохнув, напомним себе, что всё универсальное всегда было менее эффективно, чем специализированное, и пойдём покупать привычный «цех».