Виртуальные бугры

В горнолыжном мире термин «виртуальные бугры» распространен, но мы не встретили в литературе более или менее подробного описания, что же они из себя представляют? Ответ на этот вопрос может иметь, как нам кажется, не только абстрактный интерес. Как и Рон Ле Мастер («На кантах», 2002), мы полагаем, что наличие виртуальных бугров сказывается на технике поворотов.

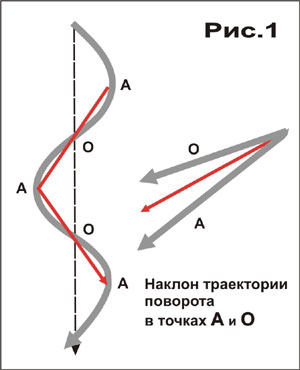
В поворотах на любом склоне лыжи едут вниз по склону как бы переменной крутизны: в сопряжениях наиболее полого, а в точках траектории, где лыжи параллельны линии склона, настолько круто, насколько крут склон (Рис.1). Переменная крутизна спуска в повороте и образует эти самые виртуальные бугры.

«Виртуальные бугры возникают вследствие округлости траектории лыж в поворотах. Поясним это гипотетическим примером на Рис.1 (слева), где изображены симметричные одинаковые повороты. Геометрически очевидно, что если склон плоский, то отрезки прямых, соединяющие наиболее разнесенные по горизонтали точки этих поворотов (красные линии), одинаково наклонены относительно плоскости горизонта. При округлении поворотов лыжи проезжают по склону соответственно выше и ниже упомянутых отрезков прямых, вследствие чего на пути лыжника возникают неровности – те самые виртуальные бугры. Кстати, именно поэтому в более округлых поворотах виртуальные бугры выше. Правая часть Рис.1 иллюстрирует наклон траектории поворота относительно плоскости горизонта в точках А и О. Вполне очевидно, что путь, по которому едет лыжник, в точках О меньше наклонен к плоскости горизонта, а в точках А - больше.

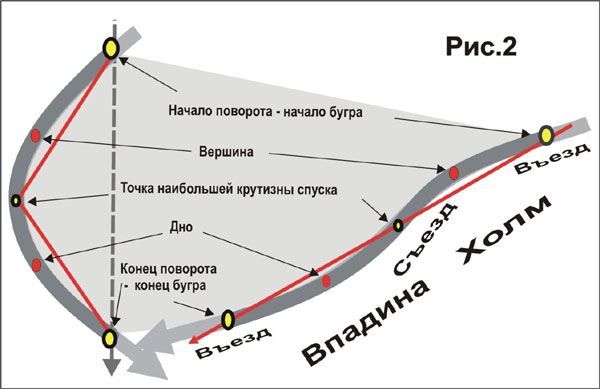«Строение» «виртуальных бугров». На Рис.2 воспроизведена примерная форма виртуального бугра, проезжаемого лыжником в крутом повороте на склоне крутизной в 40°. Мы посчитали, что более правильно связать начало бугра с началом поворота (в его «классическом» виде), то есть виртуальный бугор начинается в точке сопряжения поворотов и заканчивается в следующей точке сопряжения. В этом случае рельеф всего бугра представлен «холмом» и следующей за ним «впадиной». Холм и его вершина соответствуют верхней части поворота, а впадина с дном – нижней. Для упрощения мы считаем верхнюю и нижнюю части поворотов симметричными (хотя такое встречается нечасто). Поэтому на наших рисунках холм и впадина одинаковы по форме и размерам, но противоположно ориентированы.

Самым пологим и почти прямолинейным участком является въезд на холм бугра в зоне сопряжения поворотов. Съезд с виртуального бугра круче въезда и расположен между вершиной и дном. Наиболее крутой участок съезда (крутизна его такая же, как у склона) также практически прямолинеен, хотя и образуется сильно искривленной частью поворота. Эта «почти прямолинейность» спуска с холма виртуального бугра обусловлена тем, что повороты лыж при сравнительно небольших углах спуска (углах между направлением движения лыж и линией падения склона) мало сказываются на крутизне спуска. Например, на 40 – 30 – 20-градусных склонах крутизна спуска уменьшится на малозаметные 0,50 при поворотах на 8 – 10 – 12° относительно линии падения склона. Т.е. в области линии падения склона крутизна спуска в пределах вполне заметных поворотов на 16 – 20 – 24° близка к крутизне склона.

Различие между крутизной спуска на восходящей и нисходящей части виртуальных бугров увеличивается в закрытых поворотах и на более крутых склонах. В очень закрытом повороте на 120° (60° + 60°) на склоне в 40° наиболее пологий участок въезда на бугор (область сопряжения) имеет крутизну всего около 19°. А разница крутизны спуска между наиболее крутым и наиболее пологим участками бугра весьма заметна - около 21° (Рис.1).

Где расположены вершины и дно бугров. Вершины и дно виртуальных бугров легко найти графически и даже непосредственно на склоне. Они находятся в точках дуги, наиболее отдаленных от прямых, соединяющих точки сопряжения с наиболее разнесенными по горизонтали точками поворота (Рис.1 и 2).

Нам кажется важным подчеркнуть, что вершины виртуальных бугров не совпадают с точками сопряжения поворотов, хотя по ощущениям именно сопряжения могут восприниматься лыжниками как вершины. Аналогично и дно впадин расположено не там, где лыжи едут вниз наиболее круто.

Интересно, что вершины и дно впадин виртуальных бугров расположены приблизительно в точках поворота, где лыжи повернули соответственно на ¼ и ¾ от угла всего поворота. Для примера: в целом повороте лыжи повернули на 80° (угол между направлением движения лыж в точках сопряжения в начале и конце поворота). Тогда вершина и дно виртуального бугра соответствуют точкам траектории, где лыж повернули на 20° и 60°.

Высота виртуальных бугров зависит, как уже говорилось, от крутизны склона, «округлости», «закрытости» и длины поворота. Высоту можно приблизительно (а точно и не нужно) определять даже непосредственно на склоне. А тем более – на рисунках. Ведь нетрудно примерно оценить, насколько вершина и дно впадины бугра на склоне соответственно выше и ниже (по вертикали) соответствующих точек на упомянутых соединительных линиях.

Ориентировочные значения высоты виртуальных бугров «средней округлости» в поворотах на разных склонах приведены в таблице.

Поворот Склон	Открытый поворот 40°	Средний поворот 80°	Закрытый поворот 120°
10° пологий	0,02 – 0,05	0,06 – 0,15	0,13 – 0,32
20° средний	0,03 – 0,07	0,12 – 0,30	0,26 – 0,65
30° крутой	0,05 – 0,12	0,20 – 0,50	0,36 – 0,90
40° очень крутой	0,05 – 0,12	0,20 – 0,50	0,36 – 0,90

- расстояния между воротами принимаем равными 10 м в слаломе, 25 м в гиганте.
- первые числа в ячейках показывают высоты (в метрах) виртуальных бугров в слаломе, вторые - в гиганте.

Из таблицы видно, что на пологом склоне в открытом повороте высота виртуальных бугров равняется несущественным единицам сантиметров. Но на крутых склонах в закрытых поворотах виртуальные бугры достигают высоты около полуметра в слаломе и 1 метра в гиганте. В наиболее длинных поворотах слалома и тем более гиганта, особенно когда лыжник сильнее округляет траекторию, виртуальные бугры могут быть еще выше!

Средняя крутизна спуска и виртуальных бугров. Очевидно, в поворотах лыжник спускается по траектории переменной крутизны, которая в среднем более полога, чем склон. Непосредственно на склоне, если он ровный, средняя крутизна спуска лыжника в повороте равна крутизне прямой, связывающей наиболее разнесенные по горизонтали точки двух сопряженных поворотов. Иными словами, чтобы «увидеть» среднюю крутизну пути нужно «зрительно прострелить» от внутреннего флага одного поворота на внутренний флаг следующего.

Отрывающая и вдавливающая центробежные силы. Езда по виртуальному бугру приводит к появлению дополнительных, «вертикальных», центробежных сил, направленных перпендикулярно склону (Рис.3). На выпуклой части бугра эти силы уменьшают давление лыжника «в склон», а на вогнутой – увеличивают его. Поэтому назовем их соответственно «вдавливающей» и «отрывающей» силами. Они максимальны в наиболее криволинейных областях виртуальных бугров – на вершине и дне и плавно уменьшаются до нуля в прямолинейных зонах. На крутом склоне в быстром закрытом повороте данные силы весьма заметны. Иллюстрацией отрывающей силы может служить хорошо известный «подхлест», описанный еще Жубером: в верхней части быстрого закрытого поворота на крутом склоне лыжи легко отрываются от снега.

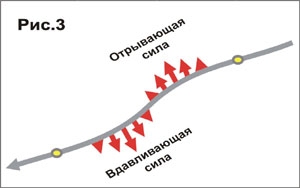Мы оценили ориентировочную величину этих вертикальных центробежных сил. Для простоты изложения расчеты упускаем. На склонах крутизной 10 – 20 – 30° в крутых поворотах отрывающая сила весьма заметна, составляя (в максимуме!) около 17 – 32 – 43%! от силы тяжести. Эти значения, но с обратным знаком, могут быть перенесены и на впадину виртуальных бугров.

Однако, как и полагается, все сложнее. Представленные величины отрывающей и вдавливающей сил справедливы только для «нижней части лыжника», т.е. лыж, креплений, ботинок и стоп, которые более или менее точно повторяют рельеф виртуальных бугров. А «верхняя часть» и центр массы (ЦМ) вследствие наклона и движений лыжника лыжника внутрь поворота перемещается иначе. ЦМ лыжника в крутом повороте за счет наклона всего тела приближается к склону, иногда очень сильно. Очевидно, что перемещение ЦМ, обусловленное таким наклоном, накладывается на рельеф виртуального бугра. Назовем траекторию, получающуюся подобным наложением, «суммарным виртуальным бугром», или «виртуальным бугром ЦМ».

Примерная его форма изображена красной линией на Рис.4. На нем видно, что рельеф суммарного виртуального бугра выражен сильнее, чем у виртуального бугра «обычного». Вследствие этого вертикальные центробежные силы должны заметно изменяться, в частности, увеличиваться.

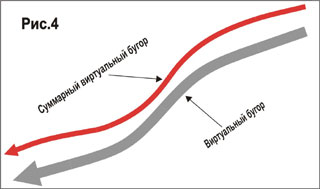Во всяком случае, ясно, что силы, возникающие при проезде на скорости крупных виртуальных бугров, заметно влияют на баланс всех сил, действующих в повороте. Причем форма суммарного виртуального бугра определяется не только наклоном лыжника внутрь поворота, но и сгибанием и разгибанием ног и туловища, т.е. зависит от техники прохождения поворотов.

Заключение. Надеемся, наша работа показалась читателю интересной. Ясно, что силы, возникающие при проезде на скорости крупных виртуальных бугров, заметно влияют на баланс всех сил, действующих в повороте. Самый важный практический вопрос, как лучше использовать рельеф виртуальных бугров в слаломе и гиганте, отчасти разобран в статье по активному мышечному ускорению, но в целом остается открытым.

Автор: Александр ГАЙ