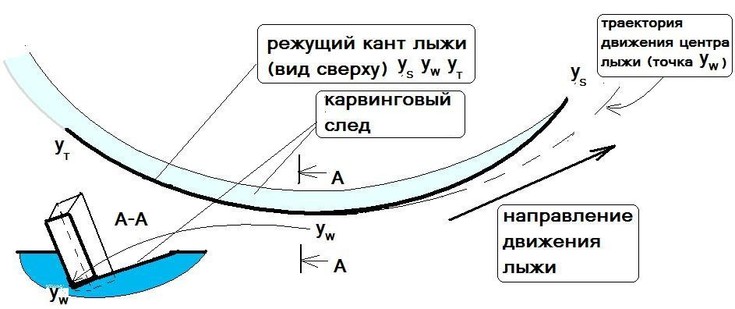
Ответы на эти вопросы чрезвычайно важны. От этого зависит как контроль скорости при катании на лыжах, так и общая безопасность лыжника. Но горнолыжная наука до настоящего времени не смогла дать ответов на эти вопросы. В данной статье эти ответы имеются.
АННОТАЦИЯ.
В статье предложена наглядная теоретическая модель, согласно которой величина максимально возможного угла закантовки не зависит от величины нагрузки на лыжу, а определяется только физико-механическими свойствами снега на слоне и направлением приложенной к лыже нагрузки и не зависит от величины этой нагрузки. Умение же лыжника прикладывать к лыже нагрузку в нужном направлении зависит только от его мастерства.
Модель позволяет просто и с достаточной точностью оценить величину максимального возможного угла закантовки лыжи, при котором лыжа в резаном повороте еще держит склон и не проскальзывает в боковом направлении, для конкретного склона и состояния снега на нем.
Предложенная модель, использует и адаптирует уже известные и апробированные профильным научным сообществом модели, гипотезы и экспериментальные данные.
Согласно представленной модели, максимальный угол закантовки лыжи, равен в точности удвоенному углу внутреннего трения снега, который формирует соответствующий склон, увеличенному на угол загрузки лыжи. Угол загрузки лыжи для равновесного карвингового поворота с большой точностью равен так называемому углу ангуляции, который количественно характеризует степень коленной и бедренной ангуляции лыжника (Браун (2007) Рейд (2010)).
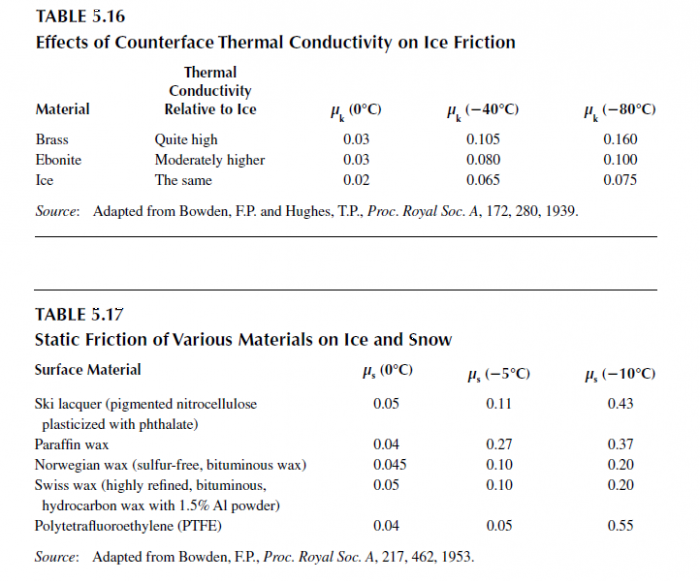
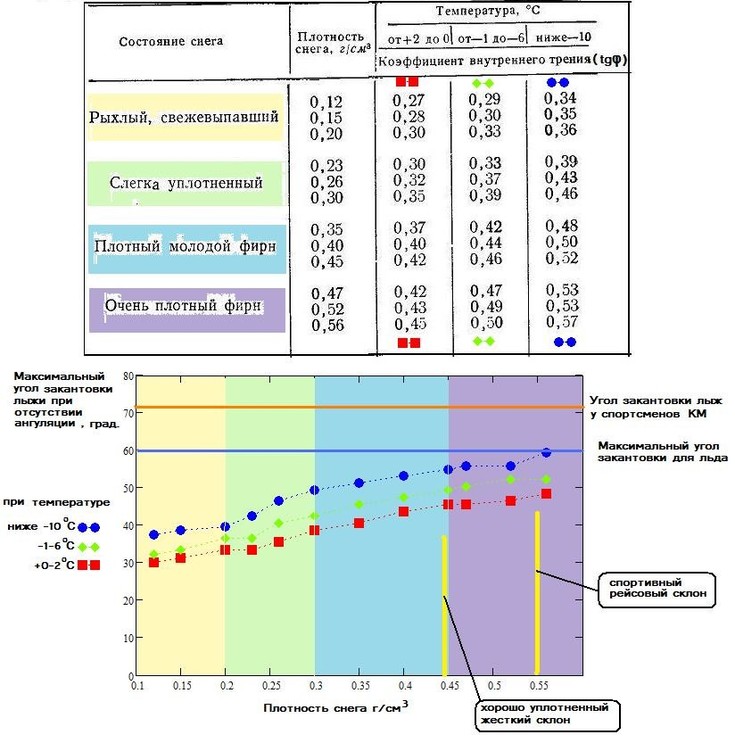
Значения коэффициента внутреннего трения снега хорошо известны. Некоторые данные, адаптированные из энциклопедии, мной обработаны в соответствии с предложенной моделью и представлены графически.
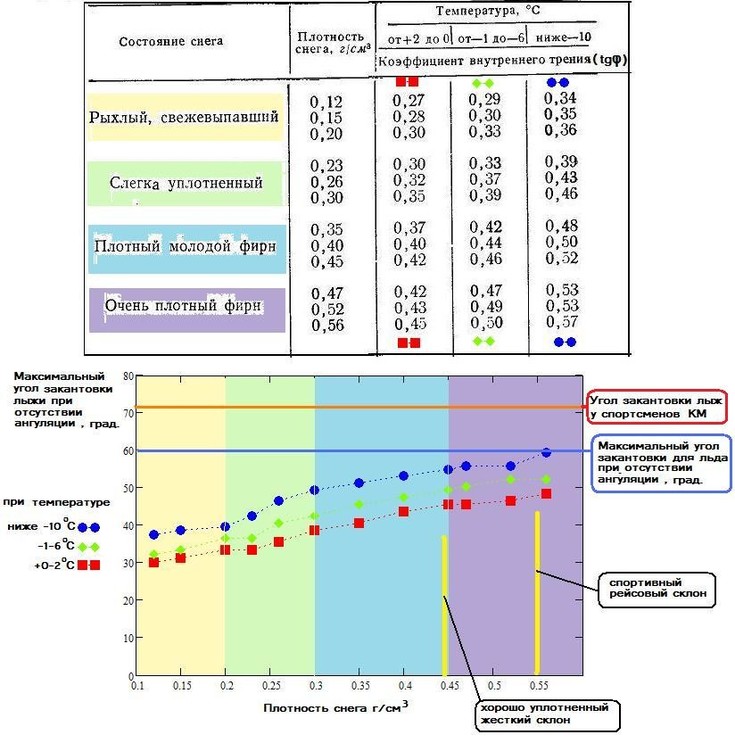
На графике представлены значения максимальных углов закантовки, при которых теоретически еще возможен карвинг при полном отсутствии ангуляции - когда лыжник едет в позе "столбового заклона" с опорой только на внешнюю в повороте лыжу.
Видно, что максимальные углы закантовки для этого случая имеют сравнительно небольшие значения - 35-60 град., которые зависят от плотности конкретного снежного покрова и температуры. В зависимости от действий лыжника этот параметр может быть увеличен. Эти действия связаны с умением лыжника загружать лыжу в "правильном" направлении и относятся к группе технических приемов, известных под общим термином "ангуляция" ("angulation", "counterbalancing" в англоязычной литературе). Высококвалифицированные спортсмены, применяя эти приемы, могут увеличить максимальный угол закантовки лыж для конкретного склона еще на 15 и больше градусов по сравнению со значениями приведенными на графике.
Максимальный угол закантовки лыжи для жесткого спортивного (рейсового) склона (плотность 0.57 г/см2) при отсутствии ангуляции у лыжника, согласно представленной теории, равен примерно 60 град. Тот же результат показали натурные эксперименты (Федерольф (2005)). Углы загрузки лыж, которых достигают высококвалифицированные спортсмены в апексе резаного слаломного поворота, за счет применения коленной и бедренной ангуляции превышают 15 град.(Рейд (2010)). Максимальные углы закантовки лыж, которых достигают высококвалифицированные спортсмены в апексе резаного слаломного и ГС поворотов составляют около 70 град.(Рейд (2010), Федерольф (2005)).
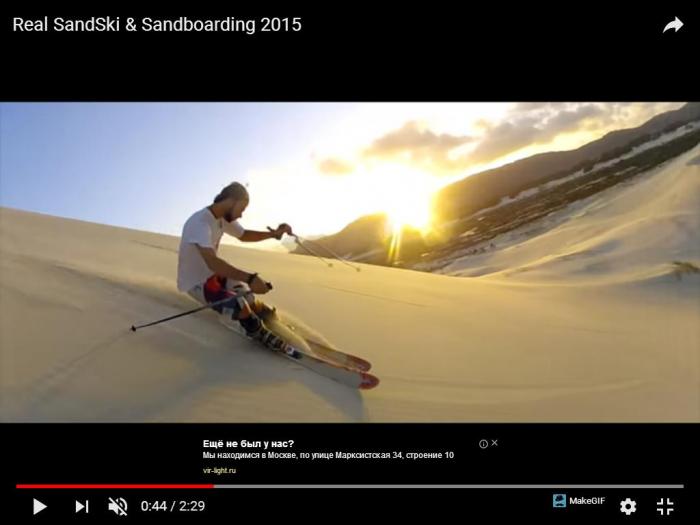
Представленная теория, с совершенно неожиданной стороны, подтверждается практикой существующих видов экстремального спорта, таких как катание на горных лыжах по песку. При этом наблюдается, что спортсмены достигают примерно тех же углов закантовки лыж, что и средний лыжник на снежном склоне - 50-60 градусов.
Именно такие максимальные углы закантовки предсказываются представленной теорией. Коэффициент и угол внутреннего трения характеризует свойства материала в сыпучем состоянии, каковым, например, является мелкий сухой песок. Угол внутреннего трения сухого мелкого песка составляет 25 градусов. Поэтому максимальныйугол закантовки лыж для техничного любителя ездить по песку составляет 50 - 60 градусов.
Полученные результаты позволяют сделать вывод, что достижение лыжником тех максимальных углов закантовки лыж, которые мы наблюдаем в спорте высших достижений невозможно без применения спортсменом группы технических приемов, связанных с созданием углового положения тела лыжника во время поворота, а также других технических приемов, позволяющих лыжнику регулировать направление загрузки лыж в повороте.
Также можно утверждать, что указанные технические приемы, которые часто объединяются в литературе под термином «ангуляция» («angulation», «counterbalancing» в англоязычной литературе) имеют основополагающее значение в общем арсенале технических приемов, как спортсменов, так и лыжников – любителей.
ВВЕДЕНИЕ
Умение лыжника достигать в повороте максимально возможных углов закантовки является чрезвычайно важным в горнолыжном спорте. Спортивные трассы ставят так что спортсмену, чтобы выиграть, нужно проходить ее с очень большими углами закантовки лыж у флагов и не допускать проскальзывания лыж в этот момент. Поэтому, возможность достижения спортсменом предельных углов закантовки в трассе является необходимым (но не достаточным) условием для победы.
Вопрос о том, при каких углах закантовки в повороте, лыжи перестают держать склон и начинают проскальзывать в боковом направлении, а также от чего этот угол зависит, важен для любого лыжника, так как от этого параметра напрямую зависит контроль скорости при катании на горных лыжах и общая безопасность лыжника при катании на лыжах.
До настоящего времени, не было предложено какой либо теории, дающей понимание того, какими параметрами определяется величина максимально возможного угла закантовки для конкретного склона, при котором лыжа в резаном повороте еще держит склон и не проскальзывает в боковом направлении.
При этом, все необходимые модели, гипотезы и экспериментальные исследования, уже имеются в профильной литературе и апробированы профильным научным сообществом.
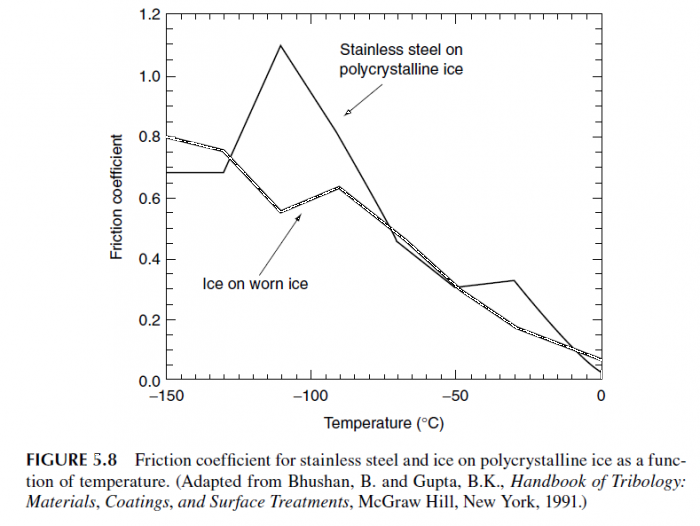
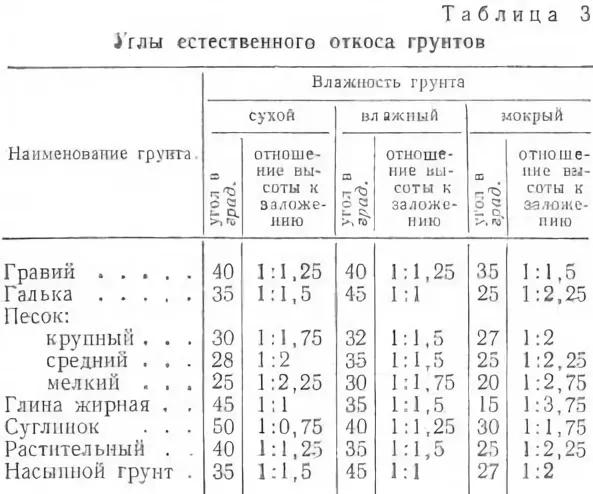
Угол внутреннего трения для сыпучих материалов имеет простое наглядное представление – это угол естественного откоса, который наблюдается при складировании этого материала. Следует отметить, что даже для горной породы угол внутреннего трения составляет всего примерно 35-40 градусов. Для льда он равен 30 градусам.
Угол внутреннего трения для очень плотного снега (плотность более 560кг/м3) или льда, из которого формируют спортивный (рейсовый) склон, равен 30 град. Угол внутреннего трения снега сильно зависит от его плотности и температуры. Данные по коэффициенту внутреннего трения снега при разных условиях хорошо известны и представлены в литературе. Ниже На Рис.1 приведена соответствующая выдержка из книги «Лавиноведение» Войтковского К. Ф. (1989)
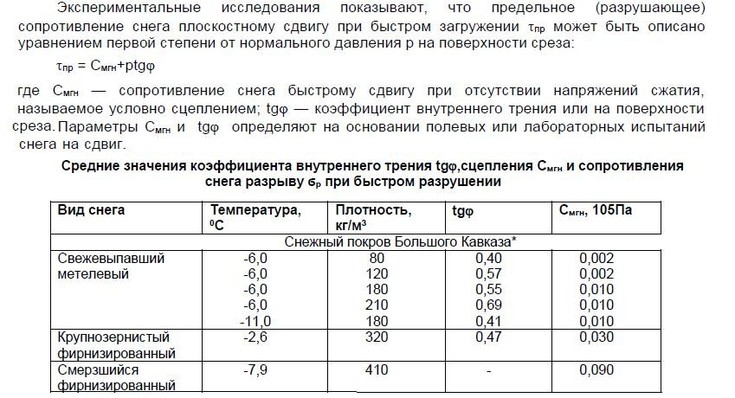
Рис.1
Исследователи уже давно считают, что боковое проскальзывание карвинговой лыжи – «skidding» - подчиняется таким же закономерностям, которые наблюдаются при обработке металла или дерева резанием («machining»).
Lieu был первый, кто используя аналогию с обработкой металла резанием, получил экспериментальные результаты для льда, которые потом он и Mote (1985) использовали для построения модели поворачивающей и режущей склон лыжи.
Brown & Outwater (1989) были первыми, кто провел подобные эксперименты со снегом. Они, используя известную в металлообработке формулу Мерчанта, пытались определить критические углы закантовки лыжи (Рис 2.), после превышения которых, закантованная лыжа начинает проскальзывать, то есть начинается «skidding» лыжи.
Рис.2 Схема эксперимента и данные, полученные Brown & Outwater (1989). Адаптировано из работы Brown (2007).
Brown (2005) ввел понятие угла ангуляции («angulation angle») (Рис.3) и пытался выяснить влияние этого параметра на минимально необходимые условия для карвинга. Но формулы, описывающей влияние этого параметра на критический угол закантовки лыжи, им получено не было.
Рис.3 Поясняющие схемы. Адаптировано из работы Brown (2007).
В дальнейшем проводились многочисленные модельные исследования, использующие аналогию процесса карвинга с обработкой металла резанием,
В натурных экспериментах Федерольфа (2005) было установлено, что закантованная лыжа начинает боковое проскальзывание уже при сравнительно небольших углах закантовки. Так сила сопротивления склона вдавливанию закантованной лыжи резко падала, а лыжа начинала проскальзывать при углах закантовки 60 град. для жесткого спортивного (рейсового) склона. Для хорошо уплотненного склона критический угол закантовки лыжи был еще меньше – 55 град.
Следует отметить, что, как Brown&Outwater (1989), так и Федерольф (2007) в своих экспериментах загружали лыжу - индентор в направлении строго перпендикулярном плоскости скользящей поверхности лыжи (Рис.2, Рис.4.).
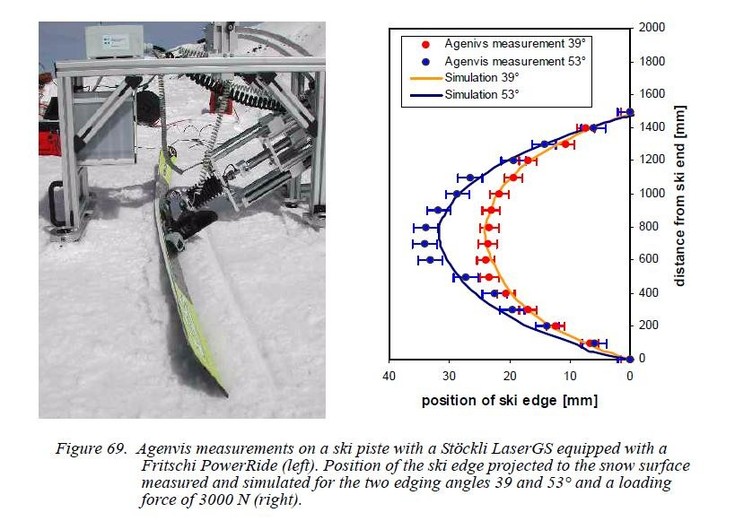
Рис.4 Экспериментальная установка в опытах Федерольфа. Адаптировано из работы Федерольф (2007).
Федерольф (2005) отмечал, что при углах закантовки 55-60 град. в его экспериментах происходило хрупкое разрушение снега и выдавливание его части индентором. Давление под индентором значительно снижалось, при этом наблюдалось хрупкое разрушение снежного покрова, появление трещин и скалывание больших кусков снежного покрова (Рис.5)
Рис.5. Выдержка из работы Федерольф (2007).
Очевидно, что по указанным причинам Федерольф (2005) не получил в своих экспериментах результатов для углов закантовки больше 60 град даже на жестком спортивном (рейсовом) склоне. Он также указывал на большой статистический разброс в данных для углов закантовки, превышающих 40 град (Рис.6).
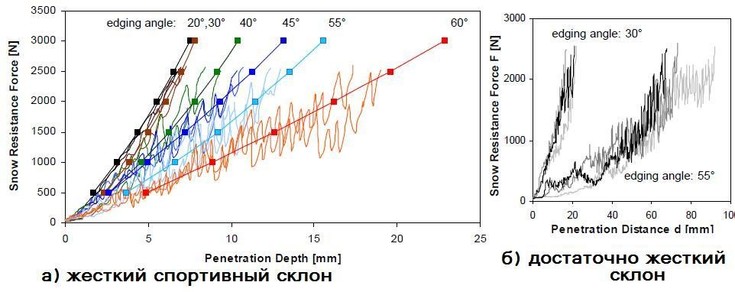
Рис. 6. Экспериментальные данные Федерольф (2007)
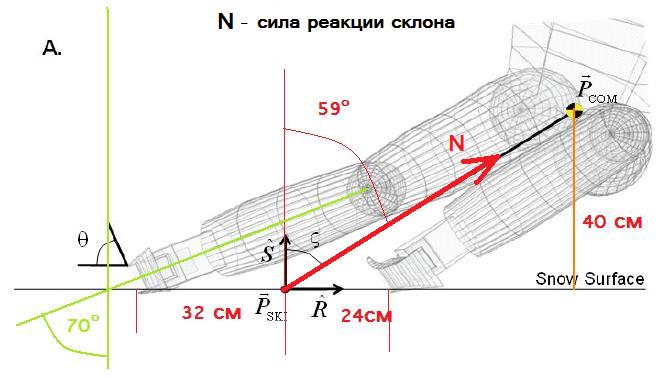
Под отсутствием у лыжника ангуляции профильное научное сообщество понимает ситуацию, когда лыжник загружает свои лыжи точно в направлении перпендикулярном скользящей поверхности своих лыж – это направление показано вектором нормали - n (синяя стрелочка) на Рис.7.
Если лыжник имеет положительную ангуляцию и соответственно загружает лыжу под некоторым углом β к направлению нормали, то максимальный угол закантовки лыжи, при котором лыжа в резаном повороте держит склон и не проскальзывает в боковом направлении, увеличивается ровно на величину этого угла β.
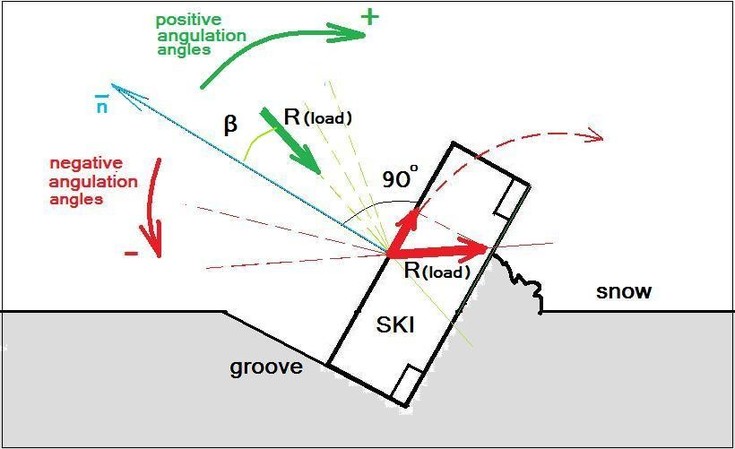
Рис.7 Схема, иллюстрирующая классический критерий врезания лыжи.
Считается, что при отсутствии ангуляции, когда лыжник загружает лыжи строго по направлению противоположному направлению синей стрелки (Рис.7), лыжа не выскальзывает из карвингового следа (groove) и режет склон (snow).
При положительных углах ангуляции сила, с которой лыжник загружает лыжу (зеленая стрелка, зеленый сектор), дополнительно вжимает лыжу в склон, при отрицательных углах ангуяции сила с которой лыжник загружает лыжу (красная стрелка, красный сектор) выталкивает лыжу из карвингового следа (красная штриховая линия) и лыжа начинает проскальзывать.
Таким образом, ангуляция улучшает «цепкость» лыжи, но считается, что и при отсутствии ангуляции лыжа также будет держать склон.
Этот подход считается общепринятым. Он описан, например ЛеМастером (1998) который предложил его в качестве критерия врезания (Рис.8).
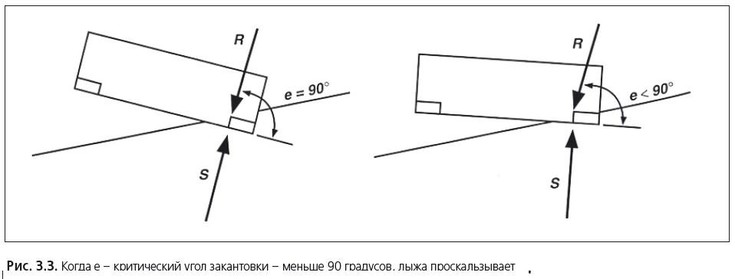
Рис. 8. Схема иллюстрирующая критерий врезания из книги ЛеМастер (1998)
Следует отметить, что направление загрузки лыж лыжником не связано напрямую с углом ангуляции. Так, даже при положительных углах ангуляции при движении лыжника, вследствие особенностей динамики движения тела лыжника в повороте, направление загрузки лыж будет находиться в красном секторе. Я неоднократно касался этих вопросов в своих статьях.
Я не буду углубляться в эту проблему в данной статье, и буду рассматривать равновесный поворот лыжника, для которого с достаточной для данной статьи точностью соблюдается соответствие между направлением загрузки лыж и «знаком» угла ангуляции лыжника.
ОПИСАНИЕ МОДЕЛИ
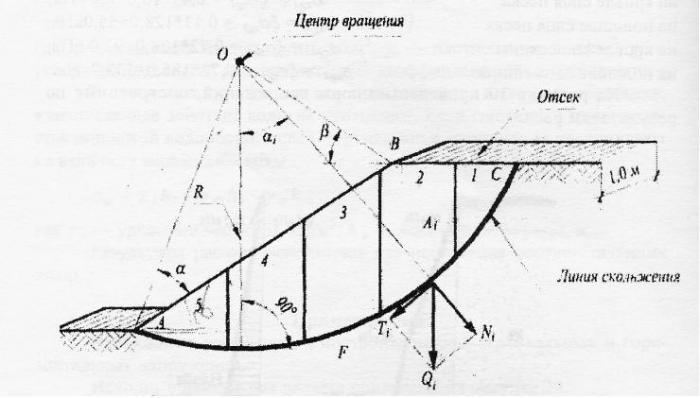
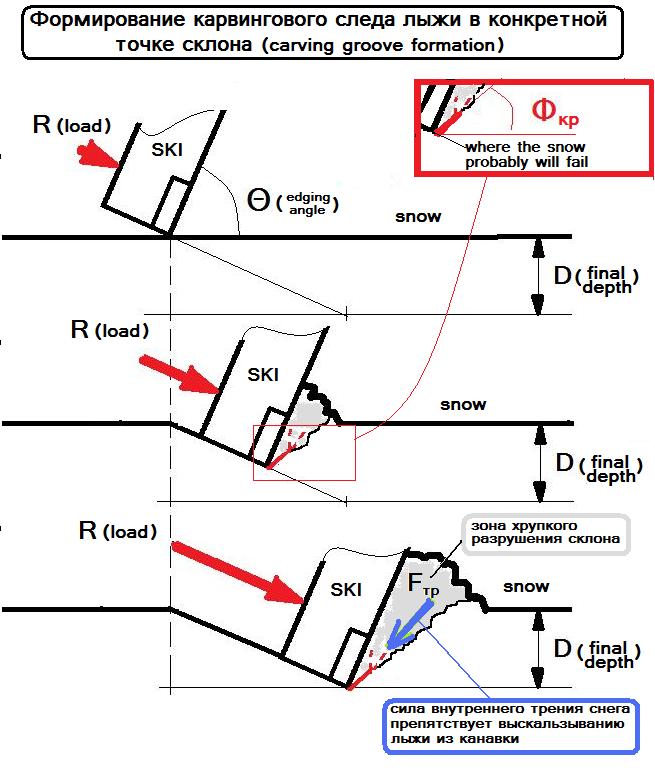
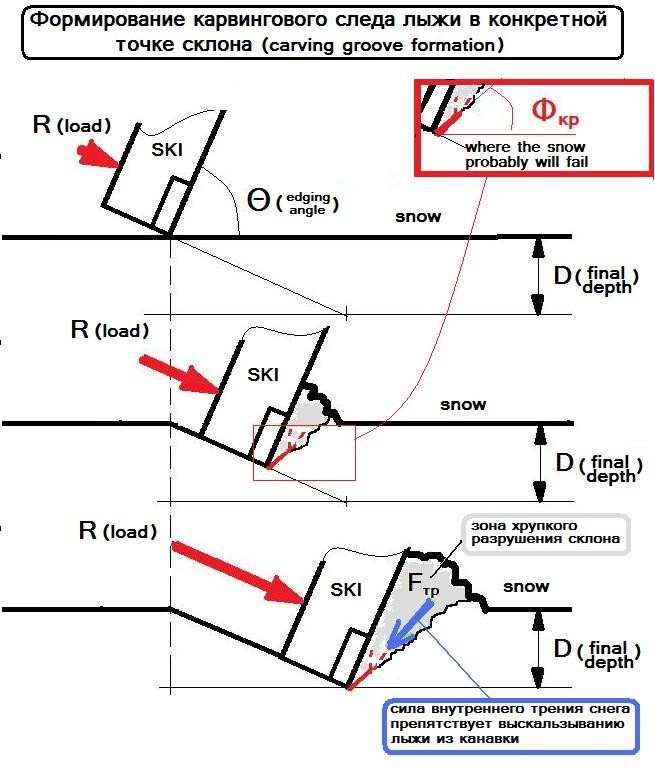
Предлагаемая в статье теоретическая концепция, в отличие от подходов других исследователей, существенно использует то обстоятельство, что при формировании карвингового следа лыжи происходит хрупкое разрушение стенки карвинговой канавки под скользящей поверхностью лыжи Федерольф (2005) . Хрупкое разрушение начинается вдоль некой плоскости наиболее вероятного разрушения. Направление этой плоскости - линия ОА на Рис.9 - определяется формулой Мерчанта (Браун (2007)).
После того, как снег вдоль линии ОА разрушился, сила R, с которой лыжник загружает лыжу, стремится выдавить лыжу вдоль линии ОА из карвинговой канавки, так как угол между направлением силы, которая загружает лыжу и линией ОА способствует этому. Выдавливанию лыжи из канавки препятствует только сила внутреннего трения разрушенного снега, расположенного вдоль линии ОА (Рис.9).
Разрушенный снег вдоль линии ОА находится под давлением, создаваемым самой же лыжей. Этим давлением, согласно формуле Кулона-Мора (формула на Рис.1.), определяется величина силы внутреннего трения снега. Коэффициент сцепления снега в данном случае равен нулю.
При увеличении угла закантовки лыжи сила внутреннего трения уменьшается, а сила выдавливающая лыжу из карвинговой канавки вдоль плоскости ОА – увеличивается и после того как она превысит силу внутреннего трения, лыжа выдавливается из канавки и начинается ее боковое проскальзывание.
Рис. 9. Схема, иллюстртрующая предложенную модель.
.
Следует отметить, что в случае неподвижной лыжи - индентора, как в экспериментах Федерольф (2005) , следует учитывать, также действие силы трения покоя снега о плоскость лыжи, которая увеличивает максимальный угол закантовки лыжи на величину удвоенного арктангенса коэффициента трения покоя между снегом и плоскостью лыжи. Величина указанного дополнительного угла для пары лыжа-снег составляет 4-5 градусов.
Соотношение, аналогичное полученной выше формуле, учитывающее силу трения между режущим инструментом и обрабатываемым материалом, известно в металлообработке как обобщенная формула Эрнста-Мерчанта для хрупких металлов.
Несмотря на очевидное математическое изящество и на то, что данная формула, учитывающая силу трения между лыжей и снегом, еще не приводилась в профильной литературе, для практики ее значение мало.
Дело в том, что в случае движущейся лыжи сила трения между лыжей и снегом будет направлена параллельно режущему канту лыжи (точка О на схеме выше) и не будет оказывать никакого влияния, как на величину силы внутреннего трения снега, так и на движение лыжи вдоль линии ОА. Известно, что сила трения скольжения направлена вдоль вектора относительной скорости контактирующих тел. Обычная скорость лыжи в направлении перпендикулярном плоскости рисунка составляет порядка 10м/с, тогда как скорость лыжи в плоскости рисунка (при формировании карвингового следа) будет составлять не более 0.2-0.4м/с.
Однако, полученная формула может быть использована для сопоставления экспериментальных данных, которые получены для неподвижного индентора Brown & Outwater (1989), Федерольф (2005) , с результатами данной статьи. Очевидно, что теоретический результат данной статьи очень хорошо соответствует указанным экспериментальным результатам
РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ.
Все результаты и выводы, в основном, представлены в аннотации.
Тем не менее, повторю, что в данной статье я рассматривал полностью статический или «лабораторный» способ загрузки лыж, который использовал в своих экспериментах Федерольф (2005) (Рис.4.) и Brown & Outwater (1989) (Рис.2.). Такой способ загрузки лыж будет наблюдаться в равновесном повороте лыжника, а именно, в повороте типа того, что выполняет велосипедист в известной школьной задаче о равномерном движении тела по окружности.
Если в резаном повороте лыжника присутствует динамика, то ситуация для лыжника-заклониста (описание в аннотации) резко ухудшается.
Вследствие особенностей динамики движения тела лыжника в повороте, направление загрузки лыж в этом случае будет находиться в «красном секторе» (Рис.7.), так как сила, с которой лыжник-заклонист действует на лыжу в динамичном резаном повороте, будет направлена из «красного» (Рис.7.) сектора при любом угле закантовки лыжи. Причем, чем меньше угол закантовки лыжи, тем труднее такому лыжнику обеспечить ее резаное ведение. Статическая ангуляция в решении этой проблемы помогает мало. Постановку этой задачи и обсуждение можно посмотреть в статье «Почему слаломист едет медленнее гигантиста или эффект абсолютно упругого склона.».
Отличие способа загрузки лыжи в опытах Федерольфа (2007) и Brown & Outwater (1989) от способа загрузки лыжи при «статической ангуляции» показано на Рис.9. Из рисунка видно как в статическом эксперименте увеличился бы критический угол при наличии ангуляции.
Рис.9.
Даже для равновесного резаного поворота сила, с которой лыжник-заклонист действует на лыжу, будет направлена из «красного» сектора, хотя в этом случае этот «красный» (Рис.7.)угол будет очень мал. Это связано с неравномерностью «поля центробежной силы». Я объяснял природу этого эффекта в статье «Что должен делать лыжник, чтобы его лыжи надежно резали склон.».
Вышеуказанные вопросы требуют подробного и отдельного рассмотрения, чему будет посвящена другая статья.
.
Следует упомянуть то, что в динамическом резаном повороте угол закантовки лыжи достаточно быстро меняется вдоль дуги поворота. Процесс формирования карвингового следа («groove») в случае «равновесного» поворота лыжника, когда угол закантовки лыж в дуге поворота не меняется, изображен на Рис. 9.
Рис.9.
Для случая динамического резаного поворота угол закантовки лыжи на этих трех рисунках (Рис.9.) будет различаться. Но, под скользящей поверхностью лыжи в любом случае будет находиться подушка из разрушенного снега. Эта подушка и будет определять максимально возможный угол закантовки лыжи, поэтому все рассуждения, которые были использованы выше при выводе формулы для максимального угла закантовки лыжи, будут справедливы и для случая динимического резаного поворота.
Также, нужно сказать, что максимально возможные углы закантовки для данного склона – это объективный параметр, который, однако, зависит от угла загрузки лыжи. Этот параметр имеет нижнюю границу, которая определяется физическими свойствами снега на склоне. Верхняя граница этого параметра определяется потенциальными возможностями лыжника.
Из статьи следует, что предельные углы закантовки у каждого лыжника, спортсмена или любителя разные и это очень сильно зависит от мастерства, например, спортсмена и тренерского ноу хау.
В литературе даже вопрос о том, какие действия спортсмена в динамическом резаном повороте регулируют направление загрузки лыж, не обсуждается. Есть достаточно простые картинки и рассуждения на тему влияния на это направление статической ангуляции и не более того.
Устойчивость лыжи от срыва в дуге - вопрос вероятностный. Критерий, полученный в статье, отражает наиболее вероятный сценарий. Поэтому общая рекомендация может быть такой - лыжник должен загружать лыжу так, чтобы у него был достаточный теоретический "запас" по отношению к тому предельному углу закантовки, который он должен использовать в трассе или в повороте при свободном катании.
Если лыжнику нужны ПРЕДЕЛЬНЫЕ углы закантовки 70 град. на жестком склоне спортивном, то он долен "нацеливаться" на 70 + "запас прочности". Поэтому к теоретически предельному углу в 60 град. для жесткого склона или льда лыжник должен "добавить" как минимум 10 град с помощью угла загрузки лыжи.
Результаты исследований Рейд (2010) показывают, что высококлассные спортсмены загружают лыжу минимум на +15град. "на всякий случай" и имеют запас прочности по предельному углу закантовки в 5град и выше.
Еще раз подчеркну главный вывод статьи - АНГУЛЯЦИИ МНОГО НЕ БЫВАЕТ!
Подробные ссылки на источники, упомянутые в данной статье содержатся в библиографиях к диссертационным работам Р. Рейда (2010) и Федерольфа (2005)
"A kinematic and kinetic study of alpine skiing technique in slalom" Reid, Robert C. (Doctoral thesis, 2010)
"Finite Element Simulation of a Carving Snow Ski" Federolf, Peter Andreas (Doctoral thesis, 2005)
)))
