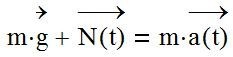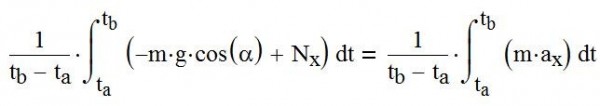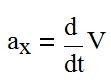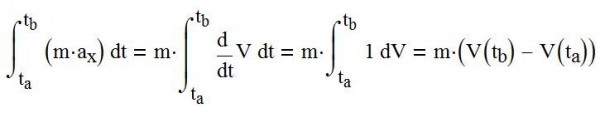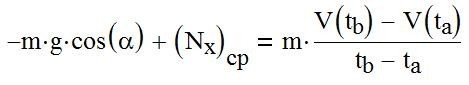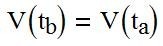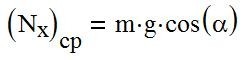Уверенно резать крутой ледяной склон - мечта любого лыжника. В статье приводятся некоторые чисто физические результаты, без учета которых будет трудно добиться достижение этой мечты.
Любой скажет - для того чтобы что-то разрезать нужно иметь нечто острое. Допустим, что это нечто острое, например, лыжи с хорошо заточенными кантами, имеется. Но разрезать что-то не надавив на режущий инструмент - затруднительно. Поэтому рассмотрим сначала вопрос - как надавить?
Глава 1. Как давить на лыжу. Или принцип сохранения давления на склон.
Как "задавить"лыжу или сноуборд (далее буду ссылаться только на лыжи, хотя все сказанное в сатье справедливо и для сноуборда)? - вопрос важный.Я столкнулся с тем что в этом вопросе отсутствует единое мнение - некоторые предлагают "давить коленом", некоторые - "давить бедром" и тп.
Однако, законы физики накладывают определенные ограничения достаточно общего характера на наше желание посильнее "надавить" на лыжу, чтобы ее не срывало в повороте. Представляется, что полезно узнать про эти ограничения поподробней, чтобы на практике не стать заложником антинаучных фантазий.
Например, существуют многочисленные поверья, связанные с техникой горных лыж. Антинаучные по своей сути.
Одно из таких поверий - в резаном повороте необходимо избегать отрыва лыж от склона - то есть "воздуха" быть не должно. Или производное от него - центр масс (ЦМ) лыжника должен двигаться на одной высоте от склона. Так как эти поверья не соответствуют физической картине мира, то следование им заводит людей, ищущих совершенства в технике горных лыж в тупик.
Прояснить вопрос нам поможет следующая ТЕОРЕМА:
Какие бы движения в течение некоторого промежутка времени не совершал лыжник на склоне, средняя сила нормального давления лыжника на склон будет равна по величине нормальной к склону составляющей силы тяжести, действущей на лыжника. При условии, что нормальная к склону составляющая сорости ЦМ лыжника в начальный и конечный момент рассматриваемого промежутка времени одинакова и что силой сопротивления воздуха можно пренебречь.
Частный случай:
Средняя сила нормального давления, которую оказывает на склон (с уклоном α градусов к горизонту) лыжник от апекса до очередного апекса любого поворота равна M*g*cos(α), где М - масса лыжника, g- ускорение свободного падения. Апекс поворота - момент поворота когда ЦМ лыжника находится на наименьшем расстоянии от поверхности (плоского) склона.
Доказательство:
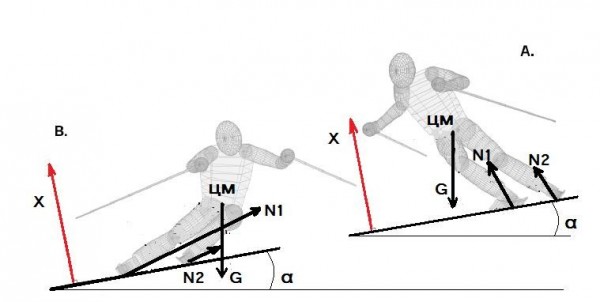
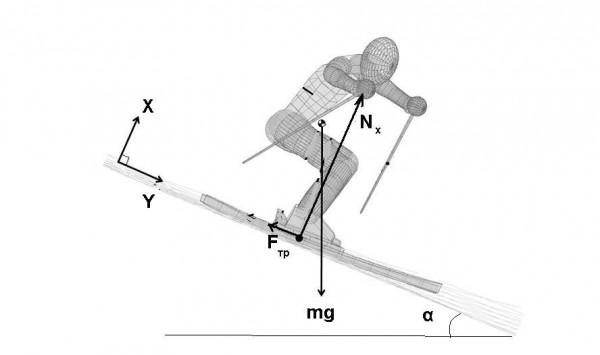
Расмотрим произвольное движение лыжника по плоскому склону с углом наклона α к горизонту в течение некоторого промежутка времени между моментами А и В. Движение лыжника будем рассматривать в системе координат, которая покоится относительно поверхности склона. Пусть ось Х этой системы координат направлена вверх по нормали к поверхности склона, а две другие оси лежат в плоскости склона. Выбранная система координат является инерциальной.
Рис. 0
Движение лыжника в выбранной системе координат происходит под действием только двух сил - переменной в общем случае во времени силы, действующей на лыжника со стороны склона Ν=Ν1+Ν2 и постоянной во времени силы тяжести G=mg.
N и G в любой момент времени связаны с ускорением - а - центра масс (ЦМ) лыжника, которая на рис. 0 не показана, известным соотношением - теоремой о движении центра масс системы материальных точек.
Векторы N и а в общем случае произвольным образом зависят от времени, но подчиняются указанному соотношению.
Рассмотрим проекцию данного соотношения на ось Х нормальную к поверхности склона
это соотношение справедливо в любой момент времени. Усредним это соотношение по промежутку времени между ta и tb
Правая часть соотношения вычисляется просто - она представляет собой сумму двух средних величин - средней величины проекции на ось Х силы тяжести, действующей на лыжника и среднюю силу нормального давления на склон (с обратным знаком). Проекция на ось Х силы тяжести, действующей на лыжника является величиной известной и постоянной во времени, поэтому ее средняя величина равна этой постоянной. Средняя сила нормального давления на склон - искомая нами величина. Вычислим интеграл в правой части, используя определение ах
где V - проекция на ось Х скорости ЦМ лыжника, получим
Для средней величины силы нормального давлениея на склон получим
Если в начальный и конечный момет проекции скорости ЦМ на ось Х равны,
то получим искомое соотношение
Теорема доказана.
Полученный результат будет справедлив для любого направления оси Х в пространстве и, также, для любого (неплоского или бугристого) склона. Под углом наклона бугристого склона к горизонту следует понимать угол наклона к горизонту некой плоскости, которая наилучшим образом "приближает" бугристый склон. Полученный результат касается ПРОИЗВОЛЬНОГО движения человека по склону.
Для резаного поворота справедлив частный случай доказанной теоремы - "эффект абсолютно упругого склона", который подробно рассмотрен в другой моей статье "Почему слаломист едет медленнее гигантиста или эффект абсолютно упругого склона".
Многих интересует влияние силы трения на скорость движения при различном "поведении" ЦМ лыжника. Существует поверье, что чем "неспокойней" ведет себя ЦМ лыжника, тем больше такой лыжник отстает от лыжника, ЦМ которого все время находится на одном расстоянии от поверхности склона. Это поверье является заблуждением. Покажем это.
Напомню читателю некоторые факты, известные еще из программы средней школы. Известно, что сила трения скольжения Fтр, действующая на лыжника со стороны склона пропорциональна силе нормального давления Nx, с которой лыжник действует на склон Fтр=μNx. Коэффициент пропорциональности μ - коэффициент трения - не зависит от массы скользящего тела, но зависит от свойств взаимодействующих поверхностей.
Без ущерба для общности рассмотрения будем рассматривать лыжника, который едет на лыжах вниз по наклонной плоскости. Коэффициент трения μ будем считать достаточно малым. Угол наклона плоскости к горизонту - α. Выберем систему координат, неподвижную относительно поверхности склона. Пусть ось Y направлена вниз по склону (по ЛПС), ось X направлена вверх перпендикулярно поверхности склона (то есть, по нормали к поверхности склона).
рис. 0.1
Рассмотрим движение лыжника ЦМ которого все время находится на одном расстоянии от поверхности склона. Эта задача, решение которой известно школьникам - лыжник будет двигаться вниз по склолну с постоянным ускорением а=gsin(α) - μgcos(α) (g - ускорение свободного падения), которое не зависит от массы лыжника.
Рассмотрим движение лыжника ЦМ которого движется произвольным образом относительно поверхности склона. Это задача, решение которой школьникам НЕ известно.
По аналогии, лыжник будет двигаться вниз по склолну с переменным ускорением A(t)=gsin(α) - μNx(t)/m (g - ускорение свободного падения, Nx - сила нормального давления лыжника на склон, m - масса лыжника ). Будем считать, что в начальный момент времени лыжники имеют одинаковую координату Y=0 (стартуют с линии старта) и одинаковую начальную скорость ЦМ равную 0. Относительное движение второго лыжника, относительно первого определяется зависимостью относительного ускорения аотн от времени. Эта зависимость дается уравнением аотн(t)=A(t)-а = μgcos(α)- μNx(t)/m. Воспользуемся доказательством сформулированной выше теоремы. Вычисляя Nx(t) из соотношения
получим для аотн(t)= -μаx(t), где аx(t) - проекция ускорени ЦМ лыжника на ось Х.
Интегрируя два раза полученное уравнение получим после первого интегрирование выражение для относительной скорости второго лыжника, относительно первого вдоль оси У - Vотн(t)=-μvx(t), где - проекция скорости ЦМ второго лыжника на ось Х. После второго интегрирования получим выражение для перемещения S(t) второго лыжника, относительно первого вдоль оси У с момента t0 до произвольного момента t - S(t)=μ(Х(t0)-X(t)), где X(t) - перемещение ЦМ второго лыжника вдоль оси Х.
Таким образом, если расстояние от ЦМ второго лыжника до поверхности склона в начальный и конечный моменты времени будет одинаковым, то лыжники на финиш придут одновременно, Движение ЦМ второго лыжника в направлении оси Х при этом может быть произвольным. Если же второй лыжник "присядет" пониже на финише, то он выиграет у первого лыжника. В любом случае, практика говорит о том, что выигрывают на трассе лыжники, которые оказывают в апексе поворота наибольшее нормальное давление на склон.
С другой стороны, скорость лыжника, который использует технику резаного поворота ПРИНЦИПИАЛЬНО ограничена как в трассе, так и в свободном катании. Это вопрос подробно изложен в другой моей статье "Почему слаломист едет медленнее гигантиста или эффект абсолютно упругого склона".
Необходимо указать одно очевидное следствие из доказанной выше теоремы, а именно, если вы хотите оказывать лыжами на склон достаточно сильное давление в определенной части поворота, то готовьтесь к тому что вам придется мириться с тем, что в другой части поворота лыжи будут разгружены, возможно, вплоть до невесомости. Или - чтобы очень сильно загрузить лыжу в цикле поворота ее надо в какой-то части этого цикла очень сильно разгрузить.
Представляется, что с точки зрения общей физической теории, указанный выше способ, а именно, достижение выраженной фазы полета в повороте, является единственной возможностью загрузить лыжу в некоторой части поворота так сильно, как вы этого хотите.
Интересно, что фаза полета при обычных условиях практически незаметна. Так, слаломный поворот происходит примерно за 0.8-0.9 сек. Если фаза полета будет продолжаться, например, 30% времени поворота, то перемещение ЦМ спортсмена по вертикали за время полета составит около 10 см.
Действительно, в фазе полета ЦМ лыжника движется с постоянным ускорением g - ускорением свободного падения и его движение описывается известными из курса школьной физики формулами о движении тела брошенного под углом к горизонту.
Без потери общности можно считать, что траектория ЦМ является симметричной, тогда перемещение ЦМ спортсмена по вертикали (по нормали к склону) можно определить по формуле S=gcos(α)t2/2 где α- угол между поверхностью склона и горизонтом, t - половина времени полета, в данном случае t=0.12 - 0.14 сек.
Точно такое же вертикальное перемещение - около 10 см - ЦМ лыжника совершает при отклонении ЦМ примерно на 25 градусов от нормали к склону при "инклинации" ЦМ во время поворота. Поэтому фаза полета может проходить и без видимого отрыва лыж от поверхности склона.
Именно так поступает Линдсей Вонн, совершая "полет над склоном" в течение почти трети цикла поворота от флага до флага и это хорошо видно на этом видео
и все это для того, чтобы должной загрузкой лыж обеспечить резанное ведение лыж в апексе поворота.
Глава 2. Что же конкретно должен делать лыжник, чтобы лыжи в активной дуге резаного поворота давили на склон сильнее?
Часть 1. Посильные каждому пассивные действия.
Ответ на вопрос Главы 2 дает теорема о движении центра масс системы материальных точек (следствие из 2-го закона Ньютона) к помощи которой мы уже прибегали выше.
Очевидно, что, чтобы увеличить в некоторый момент времени силу нормального давления на склон Νχ существует единственный способ - увеличить в этот момент проекцию ускорения центра масс лыжника на ось Х нормальную к склону (см. рис.0). То есть нормальная к склону составляющая ускорения ЦМ должна быть направлена вверх (как ось Х) и именно этот параметр лыжнику нужно каким-либо способом увеличить.
Первое, что приходит в голову - это совет лыжнику толкнуться ногами от склона. И это - правильный совет.
Однако, нас интересует ПАССИВНЫЙ способ. Для случая резаного поворота такой способ существует. Так ускорение ЦМ лыжника в дуге резаного поворота определяется законами динамики. Достаточно подробно этот вопрос рассмотрен в моей статье "Почему слаломист едет медленнее гигантиста или эффект абсолютно упругого склона".
Показано, что ускорение ЦМ лыжника в дуге резаного поворота существенно зависит от конфигурации тела лыжника и принятие наиболее выгодной конфигурации тела в апексе поворота есть надежный пассивный способ увеличить давление на склон в апексе поворота.
Что нужно делать?
1) Нужно гнуть тело (ангулировать),
2) Нужно сгибать ноги в апексе поворота
Все перечисленное - банальности, которым учили еще прадеды.
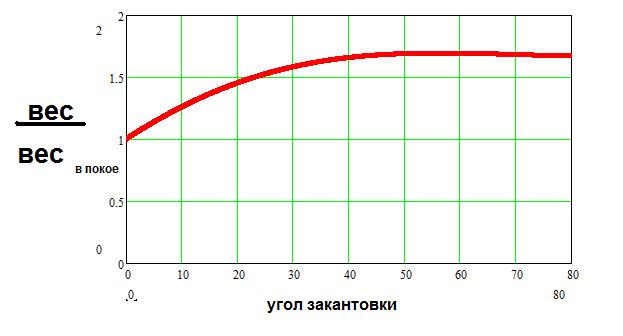
С точки зрения физики картинка зависимости величины нормального давления тела в апексе поворота от конфигурации тела лыжника при прочих равных условиях выглядит следующим образом:
Рис.1
Вычисления произведены для приближенной к реальности модели, с учетом момента инерции типичного тела лыжника. Следует отметить, что величина силы нормального давления лыж на склон "ответственна" за "подъем" тела лыжника из "старого" поворота и за "перекидывание" его в новый поворот. Из картинки видно, что советы прадедов ангулировать и работать ногами - абсолютно оправданы с точки зрения физики, а "заклонизм" - тупиковая ветвь эволюции. Также из картинки видно, что существует теоретический предел закантовки лыж в повороте - максимально допустимый угол закантовки лыж - примерно 87О для ангуляции. Этот угол для заклона гораздо меньше - 81О. Этот предел не зависит от скорости движения лыжника (то есть лыжник завалится на бок при любой скорости движения, если закантует лыжи на этот угол), но зависит от конфигурации тела лыжника.
Хочу отметить, что указанные пассивные действия лыжника являются безусловно необходимыми,но не достаточными для выполнения поворота при больших углах закантовки лыж.
Необходимо отметить, что изменение конфигурации тела лыжника не оказывает никакого существенного влияния на на величину давления лыж на склон в апексе поворота при НЕбольших углах закантовки - до 50о. Попытаюсь пояснить картинками, почему изменение конфигурации тела лыжника оказывает такое существенное влияние на величину давления лыж на склон в апексе поворота при больших углах закантовки.
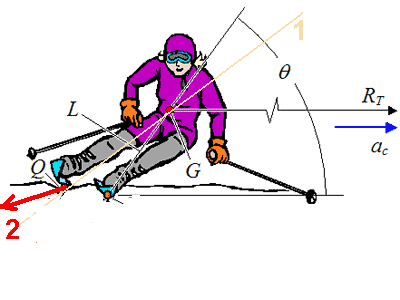
(Тело лыжника схематически изображено жирной линией. Для случая столбового заклона это - прямой отрезок (№1 на рис. 3). Для случая классической ангуляции - это изогнутый под тупым угло отрезок (№2 на рис.3). Линия О - перпендикуляр к поверхности склона опущенный в середину режущего канта лыжи(точка А на рис.2). Считаем, что лыжник - отрезок движется на зрителя.)
Во-первых, при классической ангуляции происходит уменьшению наклона (инклинации) ЦМ лыжника (точки 1 и 2 на рисунке 2) относительно режущего канта лыжи (точка А). Это приводит к изменению направления силы реакции опоры, действующей на лыжи со стороны склона и прложенной в середине режущего канта лыжи (точка А) - больше "в склон" ( красной линии 3 в случае динамического поворота приангуляции). Следует отметить, что момент ЦБС относительно ЦМ лыжника не равен нулю, поэтому при заклоне сила реакции опоры как в равновесном, так и в динамическом повороте направлена ниже ЦМ лыжника (линия 4), что делает невозможным врезание лыжи в склон. Для реализации "критерия резания" в резаном повороте лыжнику требуется некоторая ангуляция даже если он едет на лыжах с бесконечной торсионной жесткостью.
Рис. 2
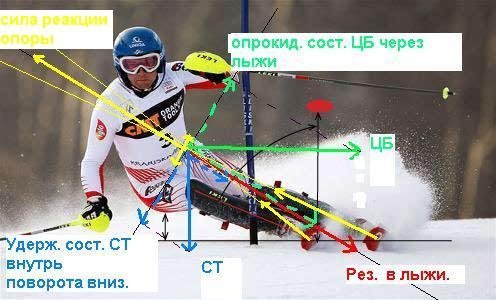
Однако, влияние этого фактора (ангуляции) не такое значительное. Гораздо большее влияние оказывает неравномерность поля центробежной силы, которую необходимо учитывать при больших углах закантовки. Происходит это из-за резкого уменьшения радиуса поворота при больших углах закантовки лыж и приближения оси вращения - нормальной к склону оси, проходящей через мгновенный центр поворота (линия 3 на рисунке 3 ) к телу лыжника. Когда же указанная ось вращения начинает проходить "сквозь" тело лыжника, как это показано на рисунке 3 для положения "заклон", ЦБС резко уменьшается вплоть до нуля. Именно это обстоятельство объясняет такое сильное расхождение кривых 1, 2, 3, 4 на рис.1.
Рис. 3
На рисунке 3 схематически показано направление и величина центробежной силы, которая действует на различные части тела лыжника (как говорили в сопромате - эпюра ЦБС) для случая "заклона" - 1 и "классической ангуляции" - 2 для достаточно большого угла закантовки лыж.
Для справки привожу графики суммарного момента ЦБС и силы тяжести, действующий на лыжника в резаном повороте, расчитанные в "университетском" приближении.(рис. 5)
Рис. 5
Из этого рисунка видно, что концепция "критической скорости" была в целом ложной.